In diesem Artikel werden wir ein echtes Wettprotokoll analysieren, dann sehen, ob das Schlagen der Schlusslinie zufällig passieren kann, bevor wir mit einem Vergleich des Wertes der Schlusslinie mit Gewinnen/Verlusten abschließen.

Indem wir die Gewinne eines Wettenden mit dem vergleichen, was zufällig hätte passieren können, können wir beginnen zu beurteilen, ob das Protokoll zu unwahrscheinlich ist, um zufällig passiert zu sein.

Der Nachteil dieses Ansatzes ist die Zeit (oder vielmehr die Anzahl der Wetten), die benötigt wird, bevor wir konkretere Meinungen formulieren können.

Pinnacle-Schlusskurs

Der Pinnacle-Schlusskurs ist die letzte verfügbare Quote, bevor ein Markt schließt (kurz vor Spielbeginn) und wird oft als Maßstab für den Erfolg von Wettenden verwendet. Wenn die Quoten, zu denen Sie wetten, höher sind als der Pinnacle-Schlusskurs, gelten Sie als "scharfer" Wettender.

Ein Wettender, der typischerweise auf Quoten um 5,0 wettet, könnte beispielsweise 2.500 Wetten benötigen, bevor er sicher sein kann, dass eine solche Leistung wahrscheinlich nicht nur auf Glück beruht - wenn er fünf Wetten pro Tag platzieren würde, würde dies mehr als ein Jahr dauern. Leider ist die Bandbreite der Möglichkeiten aufgrund des Zufalls groß und es dauert lange, bis das Gesetz der großen Zahlen seine Wirkung entfaltet.

Glücklicherweise gibt es einen alternativen Ansatz, den ich bereits erwähnt habe, als ich untersuchte, was die Schlusslinie über die Gewinnerwartung aussagen kann. Es gibt überzeugende Beweise dafür, dass die Marge, mit der Sie die Schlusslinie schlagen, ein zuverlässiger Indikator für Ihre Rentabilität ist.

Wenn Sie die Schlusslinie um 10 % schlagen, sollten Sie langfristig einen Gewinn von 10 % über dem Umsatz erwarten, was impliziert, dass die Schlusslinie die "wahren" Chancen von Sportereignissen genau widerspiegelt. Solche Quoten werden als effizient bezeichnet.

Sicherlich gibt es profitable Wettende, die es nicht schaffen, die Schlusslinie zu schlagen und daher gegen diese Hypothese argumentieren. Für diese muss es zwei Möglichkeiten geben: Entweder liegen sie falsch und haben Glück und werden zur Mitte zurückkehren, oder die Hypothese der effizienten Schlusslinie ist nicht ganz korrekt und es gibt Linien, die systematisch von solchen Wettenden identifiziert werden und die die "wahren" Preise nicht erreicht haben.

In diesem Artikel beabsichtige ich nicht, die potenziellen Schwächen dieser Hypothese zu behandeln, es reicht zu sagen, dass ich bereits eine mögliche Art und Weise diskutiert habe, wie Schlusskurse systematisch (also nicht zufällig) von voller Effizienz abweichen könnten. Dies kann ein anderes Mal behandelt werden.

Stattdessen möchte ich in diesem Artikel untersuchen, wie wir theoretisch die Schlusslinie verwenden könnten, um die Fähigkeiten eines Wettenden zu testen, vorausgesetzt, dass die Hypothese der effizienten Schlusslinie wahr ist. Schließlich hat Marco Blume, ehemaliger Trading Director bei Pinnacle, gesagt, dass die Schlusslinie im Durchschnitt sehr, sehr genau ist, dass die scharfen Wettenden sie schlagen und dass seine Händler versuchen, die effizienteste Linie mit den verfügbaren Informationen zu erreichen. Für die Zwecke des Folgenden nehmen wir ihn beim Wort.

Analyse eines echten Wettprotokolls

Das folgende Diagramm zeigt die Gewinnhistorie eines echten Wettenden mit festen Einsätzen, bestehend aus 1.214 Wetten über einen Zeitraum von 11 Wochen Anfang 2019, mit durchschnittlichen Wettquoten von 2,065 und einem Gewinn über Umsatz von 5,73 %.

Die blaue Linie zeigt die tatsächliche Leistung, die rote Linie die erwartete Leistung. Offensichtlich hat das tatsächliche Protokoll die Erwartungen übertroffen. Wie habe ich den erwarteten Gewinn berechnet?

In ihrer Wetthistorie hat der Wettende gewissenhaft alle platzierten Preise und alle Schlusskurse für diese Wetten aufgezeichnet. Wie bereits erwähnt, bietet uns das Verhältnis dieser beiden Preise eine zuverlässige Schätzung des erwarteten Vorteils des Wettenden. Natürlich enthalten beide Preise die Marge des Buchmachers. Wir müssen diese von der Schlusslinie abziehen, um eine Schätzung des "fairen" oder "wahren" Preises zu berechnen, unter der Annahme einer vollständigen Preiseffizienz bei Marktschluss.

Beim Entfernen der Marge habe ich auch die Favoriten-Underdog-Verzerrung berücksichtigt, die sieht, dass Außenseiter einen größeren Anteil an der Marge des Buchmachers anziehen als Favoriten.

Die erste Wette in der Serie wurde zum Beispiel bei 2,13 platziert. Sie schloss bei 1,85. Nach Abzug der Marge des Buchmachers lag der "wahre" Schlusskurs bei 1,89. Folglich betrug der erwartete Vorteil, den der Wettende hatte, 2,13/1,89 = 12,8 %. Das bedeutet, dass für jede 100 solcher Wetten mit 1 Einheit ein Gewinn von 12,8 Einheiten erwartet werden könnte.

Der durchschnittliche Vorteil betrug 2,19 %, was einen erwarteten Gewinn über den Umsatz von 2,19 % impliziert. Der durchschnittliche "faire" Schlusskurs betrug 2,024.

Kann das Schlagen der Schlusslinie zufällig passieren ?

Um zu untersuchen, wie und warum ein Wettender den Schlusskurs auf diese Weise schlagen kann, sollten wir zunächst die Wahrscheinlichkeit schätzen, dass dies zufällig geschieht. Dazu habe ich wieder auf eine Population von 162.672 Fußballspiel-Wettquoten bei Eröffnung und Schluss von Pinnacle zurückgegriffen, die ich in einem meiner früheren Artikel analysiert habe.

In dieser Stichprobe hatten 35,7 % der Eröffnungsquoten für Heim- und Auswärtsspiele (mit durchschnittlichen und mittleren Werten von 3,443 bzw. 2,75) theoretisch einen rentablen Vorteil gegenüber ihren "fairen" Schlusskursen. Das durchschnittliche Verhältnis von Eröffnungs- zu "fairen" Schlusskursen für diese Stichprobe betrug 0,969 %, was einen erwarteten Verlust bei festen Einsätzen von -3,1 % impliziert.

Wenn wir zufällig 1.214 Wetten aus dieser Stichprobe auswählen würden, sollten wir erwarten, dass das durchschnittliche Verhältnis 0,969 beträgt. Natürlich würden wir nicht immer 0,969 bekommen, genauso wie wir nicht immer 10 Köpfe und 10 Zahlen bekommen, wenn wir eine Münze 20 Mal werfen. Wie wahrscheinlich wäre es, zufällig eine Stichprobe auszuwählen, die ein durchschnittliches Verhältnis von 1,000 zeigt, was eine Erwartung des Gleichgewichts impliziert?

Wir können diese Frage beantworten, wenn wir die Standardabweichung der Verhältnisse von Eröffnungs- und "fairen" Schlusskursen kennen. In dieser Stichprobe betrug sie 0,114 (oder 11,4 %), was bedeutet, dass etwa zwei Drittel der individuellen Quotenverhältnisse zwischen 0,855 und 1,083 lagen, wie durch die Normalverteilung definiert.

Mit diesen Informationen können wir schätzen, wie groß die Standardabweichung im durchschnittlichen Preisverhältnis einer Stichprobe von 1.214 wäre. Das heißt, wenn wir eine große Anzahl von Stichproben mit 1.214 Wetten mit Quoten wie in meiner Population hier hätten, möchten wir die Standardabweichung im durchschnittlichen Preisverhältnis über diese Stichproben wissen.

Leser meines Artikels über die Modellierung möglicher Wettgewinne erinnern sich vielleicht daran, dass die Standardabweichung im Durchschnitt einer Wettmetrik, wie dem Ertrag oder in diesem Fall dem Verhältnis der Eröffnungs- zu Schlusskursen, umgekehrt proportional zur Quadratwurzel der Anzahl der Wetten ist. Daher kann die Standardabweichung des durchschnittlichen Preisverhältnisses hier berechnet werden, indem 0,114 durch die Quadratwurzel von 1.214 geteilt wird. Die Antwort lautet 0,0033.

Mit anderen Worten, für Stichproben von 1.214 Wetten mit Quoten wie in meiner Population hier werden etwa zwei Drittel zwischen 0,966 und 0,972 liegen. Mit dieser Zahl können wir nun die Wahrscheinlichkeit berechnen, dass ein durchschnittliches Verhältnis von Eröffnungs- zu "fairen" Preisen von 1,000 in einer Stichprobe von 1.214 Wetten zufällig auftritt, wenn der erwartete Wert 0,969 beträgt. Die Antwort ist effektiv 0 % (tatsächlich etwa 1 zu 100 Millionen Billionen, um genauer zu sein). Da 1,000 mehr als neun Standardabweichungen von 0,969 entfernt ist, wird dieses Ergebnis niemanden überraschen, der mit den Statistiken der Normalverteilung vertraut ist.

Beweis eines kompetenten Wettenden

Die Implikation dieser Analyse ist klar. Wenn ein Wettender ein durchschnittliches Verhältnis von Wettpreis zu "fairem" Schlusskurs von 1,000 zeigt, während die Erwartung bei 0,969 in einer Stichprobe von 1.214 Wetten liegt, kann dies kategorisch nicht auf Glück zurückzuführen sein. Stattdessen muss die Erklärung kausal sein; die offensichtlichste ist die Fähigkeit des Wettenden und die Reaktion des Buchmachers darauf, indem er ihre Quoten verkürzt. Wenn das nicht die Erklärung ist, brauchen wir immer noch eine andere kausale; um zu wiederholen, es kann nicht auf Glück zurückzuführen sein.

Lassen Sie uns zu unserem echten Wettenden und seinem Protokoll zurückkehren. Zunächst sollten wir anerkennen, dass seine durchschnittlichen Quoten von 2,065 signifikant anders sind als die durchschnittlichen Quoten in meiner Analysepopulation von 3,443. Wie ändert dies die Berechnungen?

Je höher die Quoten, desto wahrscheinlicher ist es, dass sie sich bewegen. Noch einmal, das ist keine überraschende Beobachtung. Wenn wir eine 80%/20% Proposition um 5% auf 75%/25% verschieben, wird sich der Favorit von 1,25 auf 1,333 bewegen (ein Verhältnis von 0,9375), während sich der Außenseiter von 5,0 auf 4,0 bewegt (ein Verhältnis von 1,25). Tatsächlich ist die Standardabweichung im Verhältnis von Eröffnungs- zu Schlusskurs proportional zum Logarithmus der Quoten. Quoten von 1,25 hatten typischerweise eine Standardabweichung von etwa 0,043, während Quoten von 5,0 einen Wert von etwa 0,14 hatten.

Ähnlich ändert sich das durchschnittliche Verhältnis von Eröffnungs- zu "fairen" Schlusskursen mit den durchschnittlichen Quoten, die ungefähr linear fallen, wenn die Quoten steigen. Quoten von 1,25 zeigen ein durchschnittliches Verhältnis von etwa 0,99, während Quoten von 5,0 eine Zahl von etwa 0,95 zeigen.

Die durchschnittlichen Quoten des Wettenden von 2,06 hätten eine Standardabweichung von etwa 0,079 und eine durchschnittliche von 0,98. Das Teilen dieser Standardabweichung durch die Quadratwurzel von 1.214 ergibt eine Zahl von 0,0022, also ist ein Verhältnis von 1,000 etwa neun Standardabweichungen von der Erwartung von 0,98 entfernt.

Schließlich sollten wir uns daran erinnern, dass der Wettende hier nicht nur den "fairen" Schlusskurs im Durchschnitt erreicht hat. Sie haben ihn um 2,19 % übertroffen. Die Chancen, dies zu tun, wenn die Erwartung -2,0 % beträgt? Etwa eine zu einem Quattuorvigintillion (1 mit 75 Nullen) oder etwa 18,5 Standardabweichungen. Dieser Wettende bewegte die Linien, und das liegt daran, dass der Buchmacher sie als jemanden erkannte, der besseres Wissen als der Rest des Marktes zu dem Zeitpunkt hatte, als sie die veröffentlichten Quoten setzten.

Es ist hilfreich, die Leser daran zu erinnern, dass ich auch versucht habe, die Häufigkeit zu modellieren, mit der ein Wettender theoretisch den "fairen" Schlusskurs übertreffen müsste, um überhaupt einen erwarteten Gewinn zu haben. Die Zahl, auf die ich gekommen bin, beträgt etwa 70 %. Unser Wettender hat den "fairen" Schlusskurs 73,5 % der Zeit übertroffen (den veröffentlichten Schlusskurs 84,2 % der Zeit).

Wert der Schlusslinie versus Gewinne und Verluste

Schauen wir uns die tatsächlichen Gewinne/Verluste (P/L) des Wettenden an. Mit meinem traditionellen Ansatz zur Signifikanzprüfung könnte eine solche Leistung zufällig etwa einmal bei 200 Wettenden passieren. Aufgrund dieser Beweise ist es wahrscheinlich, dass mehr als nur Glück im Spiel ist, aber wenn wir eine Stichprobe von 200 Wettenden hätten und dies das beste Protokoll wäre, könnten wir die Möglichkeit nicht wirklich ausschließen, dass überhaupt keine Fähigkeiten vorhanden sind.

Vergleichen Sie dies mit der Methode des Schlusslinienwerts (CLV), die ich oben beschrieben habe. Eins zu 200 gegen eins zu einem Quattuorvigintillion. Welche gibt uns zuverlässigere Informationen über die Wahrscheinlichkeit der Fähigkeiten des Wettenden?

Das folgende Diagramm vergleicht die beiden Ansätze für einen Wettenden, der auf Quoten von 2,00 wettet, und zeigt, wie viel schneller die CLV-Methode dem Wettenden bedeutende Informationen über seine Chancen gibt, ein langfristiger Gewinner mit einem erwarteten Vorteil von 2 % zu sein. Die y-Achse ist logarithmisch und misst die Chancen, dass ein erwarteter/tatsächlicher Gewinn über Umsatz von 2 % zufällig für die CLV- und P/L-Methoden auftritt.

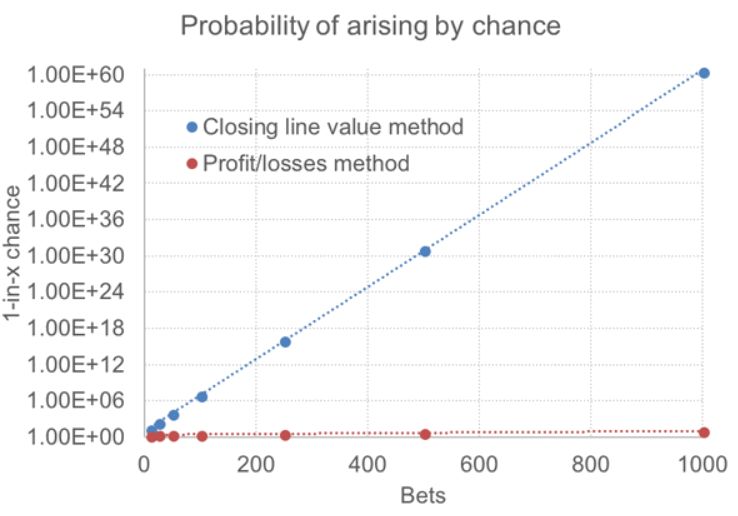
Im Vergleich zur CLV-Methode registriert die Verwendung tatsächlicher Gewinne und Verluste kaum. Selbst nach 1.000 Wetten gibt es nur eine Wahrscheinlichkeit von 1 zu 10, dass das Glück einen Gewinn von 2 % erbracht haben könnte, wo die Erwartung ein Verlust von 2 % ist. Statistiker, die Hypothesen testen, würden nicht einmal blinzeln. Sollte ein solcher Wettender einen erwarteten Ertrag von 2 % zeigen, basierend darauf, wie sie die fairen Schlusskurse der von ihnen getätigten Wetten übertreffen, würden nur 50 von ihnen die Sicherheit bieten zu wissen, dass dies einmal bei etwa 10.000 Mal passieren würde.

Natürlich könnten Sie zu Recht darauf hinweisen, dass Gewinne und Verluste real sind und Schlusslinien uns nur eine Vorstellung davon geben, was zu erwarten ist. Nach diesem Maßstab hat unser Wettender sehr gut mit einem Ertrag von fast 6 % abgeschnitten. Der entscheidende Punkt hier ist jedoch, dass es viel länger dauert, Zufälligkeit von Kausalität mit Gewinnen und Verlusten zu trennen, als mit dem Wert der Schlusslinie.

Vorausgesetzt, die Hypothese des Schlusslinienwerts ist korrekt (sie ist vielleicht nicht vollständig, aber das ist für ein anderes Mal), liefert sie einen viel zuverlässigeren Indikator für die Fähigkeiten des Wettenden als ein bloßes Wettprotokoll. Man könnte argumentieren, dass das Übertreffen der "fairen" Schlusslinie uns viel mehr über die langfristige Erwartung für diesen Wettenden sagt. Möglicherweise waren zwei Drittel der tatsächlichen Rentabilität unseres Wettenden über 1.214 in diesem Artikel präsentierten Wetten auf Glück zurückzuführen. Langfristig können sie erwarten, wieder auf 2,19 % zurückzukehren.

Schlussfolgerung

Ich weiß, dass es immer noch Wettende mit rentablen Protokollen geben wird, die es nicht schaffen, die Schlusslinie zu übertreffen und die sagen werden: "Beweist mein Protokoll nicht einfach, dass die Hypothese des effizienten Schlusslinienwerts für die Schätzung der erwarteten Rentabilität ungültig ist?" Ja, das könnte es, aber es gibt zwei Punkte, die berücksichtigt werden müssen.

Erstens, wenn ein Wettender die Schlusslinie auf die Weise übertrifft, wie unser Wettender in diesem Artikel, müssen wir dies erklären. Zufall allein kann das nicht tun, wie die Zahlen bewiesen haben. Die offensichtliche Antwort ist, dass sie fähig sind und der Buchmacher dies weiß.

Folglich, wenn ein rentabler Wettender die Linien bewegen kann, warum nicht ein anderer? Sofern ein solcher Wettender keine vernünftigen und testbaren Erklärungen dafür bieten kann, warum sie es nicht tun, muss die Wahrscheinlichkeit bestehen, dass sie einfach Glück hatten. Denken Sie daran, Sie könnten ein Wettprotokoll von 1 zu einer Million haben, aber wenn Sie der Beste unter einer Million nachvollziehbarer Wettender sind, was bedeutet das wirklich?

Zweitens, mit diesen Informationen fungiert die Schlusslinie als Maßstab, der es dem Wettenden ermöglicht, seine erwartete Leistung sehr schnell zu messen. Da selbst kleine Abweichungen von der Erwartung über Stichproben von nur 50 Wetten sehr unwahrscheinlich sind, kann der Wettende sehr schnell feststellen, ob der Markt denkt, dass er seinen Vorteil verloren hat. Das ist etwas, das mit der Analyse von Gewinnen/Verlusten allein völlig unmöglich ist. In den Worten unseres Wettenden hier: "Ich kann die CLV als Klippendetektor verwenden, damit ich langsamer werden oder meine Richtung ändern kann, um nicht abzustürzen."

Bis die Buchmacher uns die Daten zu Gewinnen/Verlusten im Vergleich zum Schlusslinienwert zeigen, werden wir nie genau wissen, wie zuverlässig ein CLV-Indikator wirklich ist. Ein großer Teil meiner Datenanalyse dazu, die im Laufe der Jahre in Pinnacles Betting Resources veröffentlicht wurde, legt nahe, dass, wenn es nicht perfekt ist, es sicherlich ziemlich gut ist.

Schließlich hat uns Marco Blume gesagt, dass scharfe Wettende die Linien bewegen. Wer bin ich, um dem zu widersprechen? Also, wenn Sie umsichtig genug sind, ein Protokoll Ihrer Wettquoten zu führen, behalten Sie auch die Schlusskurse bei, und Sie können sehr schnell feststellen, ob Ihr Buchmacher und der Markt denken, dass Sie ein Gewinner sind.