In diesem Artikel werden Sie lernen, wie verschiedene Einsatzstrategien unter Verwendung der Kelly-Formel neu interpretiert werden können. Außerdem werden die Auswirkungen auf Verlust und/oder Gewinn von Einheiten, die Asymmetrie der Renditen und die Symmetrie der Wahrscheinlichkeit erklärt.

Vor vier Jahren wurde ein Artikel im „Journal of Sports Economics“ veröffentlicht, der sich damit beschäftigte, wie ein rentabler Wettender in Situationen setzen sollte, in denen die genauen Wahrscheinlichkeiten des Gewinns nicht bekannt sind.

Die Frage, ob ein Wettender, der langfristig profitabel sein möchte, unter solchen Bedingungen überhaupt aktiv sein sollte, ist diskutabel. Dennoch erkennen viele Sportwettende an, dass sie nicht in der Lage sind, diese Wahrscheinlichkeiten genau zu schätzen.

Ihre Studie ist interessant, weil sie zeigt, wie verschiedene Einsatzstrategien als Varianten des Kelly-Kriteriums interpretiert werden können. In diesem Artikel möchte ich ihre Bemühungen zusammenfassen und untersuchen, ob ihre Entdeckungen verbessert werden können.

Neuinterpretation verschiedener Einsatzstrategien mit der Kelly-Formel

Es gibt vielleicht kein beliebteres Thema im Bereich des Geldmanagements bei Sportwetten als die Verwendung des Kelly-Kriteriums als Einsatzstrategie. Ich habe gezeigt, dass bei einer einfachen Kelly-Wette, bei der nur eine Wette gleichzeitig vor der Abrechnung platziert wird, die Strategie in der Lage ist, die Risiken zu berücksichtigen, die mit der Unsicherheit des genauen Vorteils verbunden sind, solange Sie im Durchschnitt genau sind.

Einheitsverlust

Die erste dieser Strategien ist der Einheitsverlust oder die Methode der gleichmäßigen Einsätze, bei der der Wettende bei jeder Wette dasselbe Risiko eingeht, unabhängig von den Quoten. Je höher die Quoten, desto größer ist der Einfluss auf die Bankroll im Falle eines Gewinns, aber desto geringer ist die Wahrscheinlichkeit eines Gewinns.

Wir können das Wetten auf Einheitsverluste als einen Kelly-Plan betrachten, bei dem der erwartete Wert (EV) oder die Rendite linear proportional zu den Quoten ist. Da die Kelly-Einsatzgröße durch EV / (Quoten - 1) gegeben ist (wobei EV der erwartete Wert ist, alles über 0 ist profitabel), impliziert ein Plan für Einheitsverluste, dass dieses Verhältnis konstant bleibt.

Zum Beispiel nehmen wir an, dass der EV 10 % (0,1) und die Quoten 2,00 betragen. Der Einsatz wäre 0,1. Wenn die Quoten auf 4,00 steigen, muss der EV auf 30 % (0,3) steigen, damit der Einsatz bei 0,1 bleibt. Eine Quote von 101,00 würde einen EV von 10 oder 1.000 % implizieren, was ziemlich unrealistisch erscheint. Dies würde eine wahre Quote von nur 9,18 implizieren. Kein Buchmacher würde einen so großen Fehler machen.

Tatsächlich tendieren die echten Quoten in der Grenze gegen unendlich zu einem maximalen Wert von 1 / Einsatz, in diesem Fall 10. Eine der Hauptkritiken am Einsatz bei Einheitsverlusten ist, dass er ein zu hohes Risiko bei Langzeitwetten mit geringer Gewinnwahrscheinlichkeit birgt. Für Befürworter des Kelly-Kriteriums würde dies nur Sinn machen, wenn der EV tatsächlich proportional zu den Quoten ansteigt, was, wie wir sehen können, kaum glaubhaft ist.

Einheitlicher Gewinn

Der zweite allgemein verwendete Geldmanagementplan von Wettenden ist die einheitliche Gewinnwette. In diesem Fall wird der Einsatz so gewählt, dass der Wettende unabhängig von den Quoten den gleichen Gewinn erzielt. Wenn das Gewinnziel 100 € beträgt, erfordert eine Quote von 2,00 einen Einsatz von 100 €, während eine Quote von 5,00 einen Einsatz von 25 € erfordert. Die Einsatzgröße ist proportional zum Kehrwert der Quoten - 1. In Bezug auf Kelly impliziert die Strategie des einheitlichen Gewinns, dass der EV absolut nicht mit dem Kelly-Kriterium korreliert ist; alle EV sind unabhängig von den Quoten gleich.

Einfluss des Einsatzes

Die Autoren haben eine alternative Einsatzstrategie vorgeschlagen: den Einheitseinfluss, wobei angenommen wird, dass dieser Plan besser mit der Kelly-Methode übereinstimmt. Die Einheitseinflussmethode hält den Unterschied in der Bankroll zwischen Gewinn und Verlust konstant, unabhängig davon, wie lang oder kurz die Quoten sind.

Der Einsatz des Einheitseinflusses ist proportional zum Kehrwert der Quoten, im Gegensatz zum einheitlichen Gewinn, der der Kehrwert der Quoten - 1 ist. Wenn der Einsatz 100 € bei einer Quote von 2,00 beträgt, wird der Einheitseinflusseinsatz bei einer Quote von 5,00 40 € betragen. In jedem Fall beträgt der Unterschied zwischen Gewinn und Verlust 200 € (+100 €/100 € im ersten Fall und +160 €/40 € im zweiten Fall).

Für Einheitseinflusswetten ist der EV proportional zu (Quoten - 1) / Quoten. Das bedeutet, dass der EV mit steigenden Quoten zunimmt, aber mit einer abnehmenden Rate gegen ein Limit tendiert, da dieses Verhältnis schnell gegen 1 tendiert. Wenn der EV beispielsweise 0,1 für eine Quote von 2,00 beträgt, wird das EV-Limit 0,2 sein. Obwohl dieses Szenario nicht so extrem ist wie bei der einheitlichen Gewinnwette, bei der der EV gleich bleibt, scheint es erneut die Möglichkeit höherer EV für längere Quoten zu unterschätzen.

Erfolgreiche Pferderenn-Tipper haben in der Regel deutlich höhere Renditen als diejenigen, die sich auf den asiatischen Handicap- oder Punkteverteilungsmarkt konzentrieren. Dies bedeutet jedoch nicht unbedingt, dass sie kompetenter (oder glücklicher) sind; sie haben einfach eine größere Varianz auf ihrer Seite.

In Übereinstimmung mit den Autoren zeigt die folgende Tabelle, wie sich der EV in Abhängigkeit von den Quoten für die drei verschiedenen Einsatzstrategien ändert, wobei angenommen wird, dass der EV für eine Quote von 2,00 3 % beträgt.

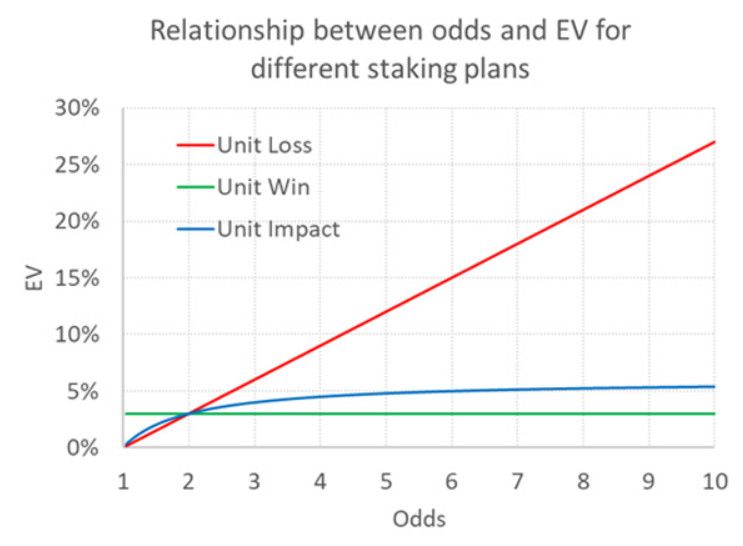
Wie bereits erwähnt, scheinen die Strategien "Einheitsverlust" und "einheitlicher Gewinn" beide unrealistische Beziehungen zwischen Quoten und EV zu implizieren.

Die Autoren analysierten die Datenbank von Wettentscheidungen einer bekannten Prognoseseite und glauben, dass die Beziehung zwischen EV und Quoten, die durch die Einheitseinflussmethode impliziert wird, am besten die beobachteten und erwarteten Renditen der Tipper widerspiegelt (letztere basieren auf den Abschlussquoten). Ich bin immer noch nicht überzeugt. Die Methode des Einheitseinflusses wird niemals einen EV produzieren, der mehr als das Doppelte des EV für Quoten von 2,00 beträgt. Gibt es eine bessere Alternative?

Überprüfung der T-Verteilung

Vor drei Jahren habe ich die Verwendung der T-Verteilung zur Bewertung von Prognostikern vorgestellt, um Glück von Können zu unterscheiden. Ähnlich der Normalverteilung (und anstelle dieser verwendet, wenn nur die Stichprobenstandardabweichung und nicht die Populationsstandardabweichung bekannt ist), ermöglicht sie die Bestimmung des Grades der Unwahrscheinlichkeit einer gegebenen Stichprobe, vorausgesetzt, der Populationsmittelwert ist bekannt.

Ich habe die T-Verteilung häufig in meiner Arbeit verwendet, um Wettenden zu helfen, die Wahrscheinlichkeit zu bestimmen, dass ihre Ergebnisse zufällig sind, vorausgesetzt, sie haben keine Fähigkeiten. Je geringer die Wahrscheinlichkeit, desto sicherer können Sie subjektiv sein, dass der Zufall nichts mit Ihren Wettgewinnen zu tun hat.

Im Zentrum dieses Tests steht die t-Statistik oder der t-Wert, aus dem die Wahrscheinlichkeiten abgeleitet werden können. Ich habe gezeigt, dass für eine Einheitsverlustwette und wenn die Quoten Ihres Rekords nicht stark variieren, diese Statistik ungefähr mit der folgenden Formel berechnet werden kann.

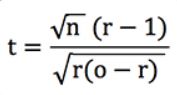
Dabei ist n die Anzahl der Wetten, o die durchschnittlichen Quoten und r die Rendite oder der ROI + 1.

Wie der z-Score, den Handicaper möglicherweise besser kennen, ist dies im Wesentlichen eine Messung der Anzahl der Standardabweichungen, die Ihre Rendite von einem erwarteten Mittelwert von Null abweicht, wenn Sie ohne Fähigkeiten und zu fairen Quoten wetten. Ein t-Wert von 2 bedeutet beispielsweise, dass eine bessere Rendite als die, die Ihr Rekord erzielt hat, nur 2,5 % der Zeit erwartet wird, vorausgesetzt, Sie haben keine Fähigkeiten. Der t-Wert ist daher eine Art Wahrscheinlichkeitsmaß. Je höher der t-Wert, desto unwahrscheinlicher ist die Beobachtung. Verwenden wir ihn, um die Wahrscheinlichkeit verschiedener EV zu bestimmen (vorausgesetzt, es gibt keine Fähigkeiten) basierend auf den Quoten, auf die wir wetten.

Die Asymmetrie der Renditen

Angenommen, Sie wetten auf ein Team mit einer Gewinnchance von 80 % und Quoten von 1,25. Angenommen, der Buchmacher denkt fälschlicherweise, die Gewinnwahrscheinlichkeit beträgt 75 %. Er macht eine Promotion und hat keine Marge. Seine Quoten sind 1,333. Daher beträgt Ihr EV 6,667 % (1,333/1,25 - 1 oder 0,80/0,75 - 1).

Betrachten wir nun ein zweites Szenario: Die echte Gewinnchance beträgt 20 % (faire Quoten von 5,00), aber der Buchmacher schätzt sie auf 15 % (veröffentlichte Quoten von 6,667). Diesmal beträgt Ihr EV 33,

33 % (6,667/5,00 - 1 oder 0,20/0,15 - 1). Der Unterschied im erwarteten Gewinnprozentsatz zwischen Ihrer Schätzung und der des Buchmachers ist derselbe, aber der EV ist fünfmal höher. Es scheint, dass in Bezug auf EV gleichwertige Fehler bei höheren Quoten stärker bestraft werden. Aber wie wahrscheinlich sind diese Fehler?

Die Symmetrie der Wahrscheinlichkeit

Schreiben wir die obige t-Score-Formel um (angenommen, alle unsere Wetten haben die gleichen Quoten o). Da wir wissen, dass r = q / p ist, wobei p die implizite Wahrscheinlichkeit der Quoten des Buchmachers ist (d. h. 1/o) und q Ihre geschätzte Wahrscheinlichkeit ist (die „wahr“ ist, wenn Ihr Prognosemodell genau ist), können wir zeigen, dass:

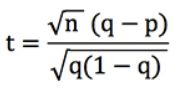
Angenommen, n, unsere Anzahl der Wetten, beträgt 100. Für q = 0,8 und p = 0,75 ist t = 1,25. Ebenso für q = 0,2 und p = 0,15 ist t = 1,25 ebenfalls. Angenommen, der Buchmacher und nicht unser Modell ist tatsächlich korrekt, würde ein solcher t-Wert einer Ergebniswahrscheinlichkeit von 10,7 % entsprechen (unter Verwendung der Excel-Funktion =TDIST).

Bei 100 Wetten sollten wir eine Rendite von über 6,667 % für Quoten von 1,333 oder über 33,33 % für Quoten von 6,667 10,7 % der Zeit erzielen. Größere Renditen bei höheren Quoten sind genauso wahrscheinlich wie kleinere Renditen bei kürzeren Quoten; deshalb haben Rennprognostiker die Illusion, besser zu sein als Handicapper oder schlechter, wenn sie Verluste machen.

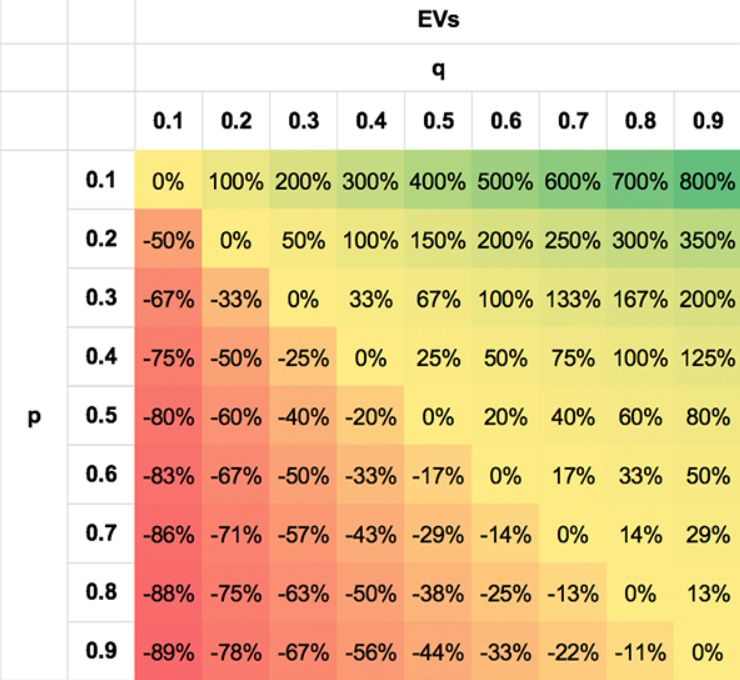
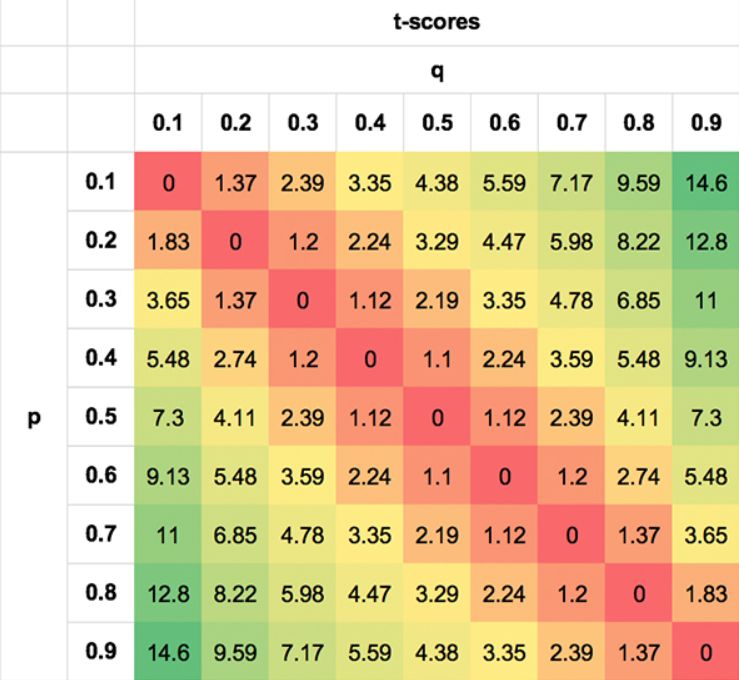
Ich habe versucht, diese Symmetrie der Wahrscheinlichkeiten mit den folgenden Tabellen zu veranschaulichen. Die Werte sind extrem, um den Punkt zu verdeutlichen; offensichtlich wird kein Wettender in der Lage sein, dies in den meisten Szenarien so gut oder schlecht zu tun.

Das erste zeigt die Asymmetrie des EV für verschiedene Paare p, q. Das zweite zeigt die Symmetrie der t-Scores. Der zweite zeigt die Symmetrie der t-Scores. Ich habe die absoluten t-Scores angegeben (das negative Zeichen für negative EV entfernt, wenn q < p) zur Klarstellung. Nicht nur ist ein Paar p, q von 0,3/0,7 genauso wahrscheinlich wie ein Paar 0,7/0,3, sondern auch Paare wie 0,7/0,5 und 0,3/0,1, 0,8/0,7 und 0,2/0,1 aus den oben beschriebenen Gründen.

Eine neue EV-Quotenfunktion

Für eine gegebene Quote und einen gegebenen EV gibt es eine t-Wahrscheinlichkeit (die sich verdoppelt, wenn die Anzahl der Wetten vervierfacht wird). Wir können die t-Score-Formel umstellen, um sie in Bezug auf r auszudrücken. Dies führt zu einer ziemlich schrecklichen Quadratik mit einer noch schrecklicheren Lösung.

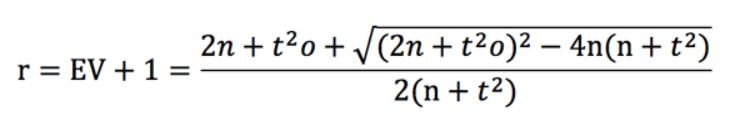
Dies ist eine viel unangenehmere Lösung als (Quote - 1) / Quote, aber lassen Sie uns sie trotzdem für das Szenario darstellen, bei dem EV = 0,03 und Quote = 2,00. Diese Grafik wird unten zusammen mit den vorherigen EV-Funktionen für Einheitsverlust, einheitlichen Gewinn und Einheitseinfluss-Einsätze gezeigt.

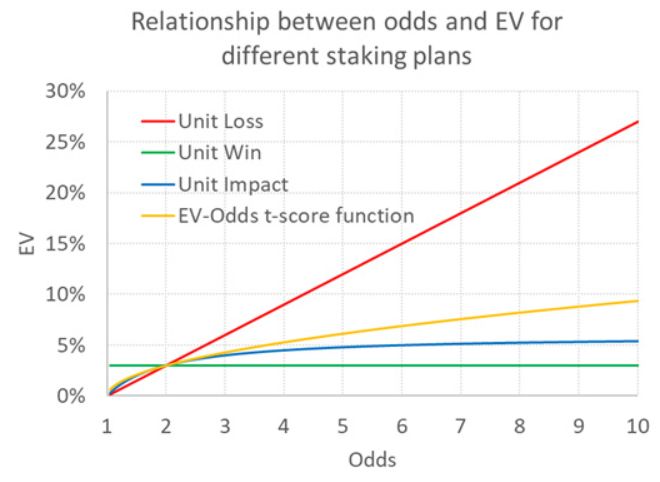
Obwohl die Funktion schwierig zu schreiben ist, ist sie intuitiver, da sie die erwarteten Renditen in Bezug auf die statistische Wahrscheinlichkeit interpretiert. Für Einheitseinflusswetten kann der EV niemals mehr als 6 % betragen, wenn er 3 % für Quoten von 2,00 beträgt. Mit meiner Funktion kann er jedoch unbegrenzt wachsen, wenn auch nicht so unrealistisch schnell wie bei Einheitsverlustwetten, sondern in Übereinstimmung mit dem, was die statistische Varianz vorhersagt. Für Quoten von 10 beträgt er 9,4 %, für Quoten von 50 beträgt er 23,3 % und für Quoten von 1.000 beträgt er 150 %.

Eine offensichtliche Kritik ist, dass diese Funktion, basierend auf dem T-Score, annimmt, dass der Wettende keine Fähigkeiten hat. Sie drückt einfach die Wahrscheinlichkeit aus, dass Dinge passieren, vorausgesetzt, keine Fähigkeiten sind vorhanden. Aber das ist eine Fehlinterpretation; selbst in Anwesenheit von Fähigkeiten gelten die gleichen statistischen Gesetze im Zusammenhang mit der Varianz.

Die Position der orangenen Kurve würde sich ändern, aber die Form würde gleich bleiben. Ich habe unten einige mögliche Trajektorien für Wettende mit unterschiedlichen Graden von Glück oder Können illustriert. Die ursprüngliche Kurve für den Wettenden mit einem EV von 3 % für Quoten von 2,00 ist weiterhin in Orange dargestellt.

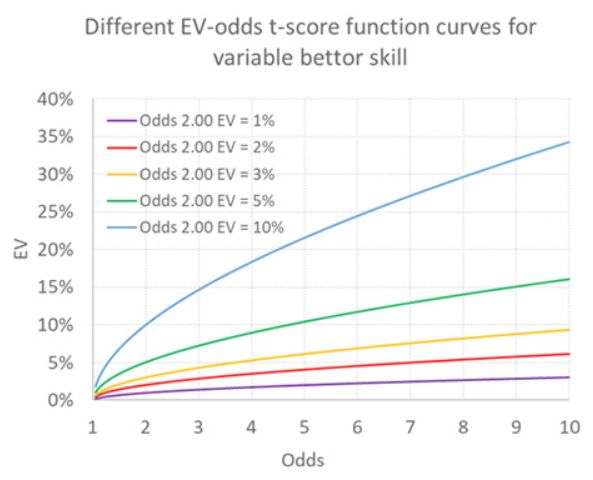
Eine weitere Kritik könnte sein, dass wir auch annehmen, dass jede Fähigkeit unabhängig von den Quoten ist, d. h. dass sie unabhängig von den Quoten gleich ist. Angesichts von Marktineffizienzen wie dem Favoriten-Außenseiter-Bias ist diese Annahme möglicherweise nicht angemessen.

Testen der Funktion

Können wir die Gültigkeit dieser neuen EV-Funktion testen? Mein „Wisdom of the Crowd“-Wettsystem, das diejenigen, die mir regelmäßig auf Twitter und Football-Data folgen, gut kennen, verwendet die effizienteren Quoten von Pinnacle, um den verfügbaren EV in den Quoten anderer Buchmacher zu schätzen.

Aus einer Datenstichprobe von Quoten aus europäischen nationalen Ligaspielen seit der Saison 2012/13 habe ich 55.237 Gelegenheiten gefunden, bei denen ein profitabler EV (>0) verfügbar war. Der Durchschnitt betrug 2,20 % (zur Erinnerung, die tatsächliche Performance bei Einheitsverlusten betrug 1,77 %, weit innerhalb der statistischen Fehlermargen des Modells), bei durchschnittlichen Quoten von 3,30. Mit diesen Zahlen können wir meine quadratische Lösungsgleichung verwenden, um eine EV-Funktionskurve wie die oben genannten zu erstellen. Diese wird in der folgenden Grafik in Orange dargestellt.

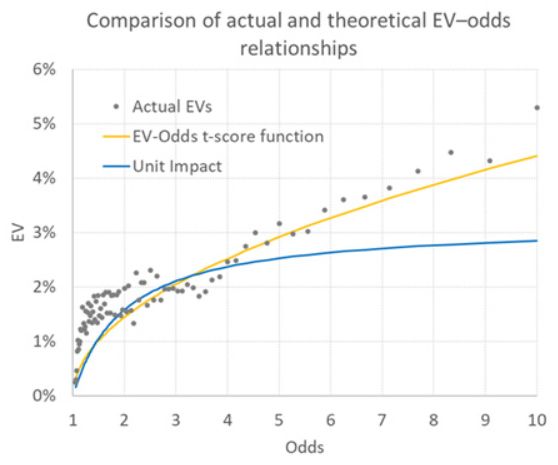
Vergleichen Sie diese Kurve einerseits mit den tatsächlichen EV, die anhand der erwarteten Gewinne von 1 % basierend auf den Quoten berechnet wurden (im Diagramm als Quoten dargestellt), und andererseits mit der EV-Funktionskurve, die durch die Einheitseinfluss-Einsatzmethode vorhergesagt wird. Obwohl die Übereinstimmung nicht perfekt ist, sagt die t-Score-EV-Funktion möglicherweise besser die ungefähren EV basierend auf den Wettquoten voraus.

Ein Fazit

Die aufmerksamen Leser könnten sich nun fragen: Was ist der Sinn der Verwendung einer EV-Funktion zur Vorhersage des EV für verschiedene Quoten, wenn Ihr „Wisdom of the Crowd“-Modell dies explizit für jede Wette tut? Dies ist in der Tat eine gültige Frage, und ein großer Teil dieses Artikels könnte daher als eher theoretisch angesehen werden.

Dennoch haben selbst präzise Modelle (im Durchschnitt) eine epistemische Unsicherheit bei jeder Wette. Darüber hinaus macht die zufällige Unsicherheit (oder inhärente Unsicherheit) die Bewertung der tatsächlichen Gewinnwahrscheinlichkeiten praktisch unmöglich.

Das Ziel dieser Übung war es daher, wie auch die Autoren, zu illustrieren, wie man versuchen kann, seinen EV näherungsweise zu schätzen, wenn man diese quantitativen Unsicherheiten anerkennt, wenn das Prognosemodell die Gewinnwahrscheinlichkeiten nicht explizit schätzt oder wenn die Vorhersagemethode qualitativer Natur ist und auf Intuitionen statt auf Datenanalyse basiert. Wenn Sie Ihre Wahrscheinlichkeiten kennen, können Sie mit dieser Methode Ihren EV schätzen; wenn Sie Ihren EV kennen, können Sie dann die Kelly-Wettgröße bestimmen, die Sie verwenden sollten.

Diese t-Score-Methodik mag kompliziert erscheinen, aber ihre Ergebnisse basieren auf einer intuitiveren Interpretation der Beziehung zwischen Gewinnwahrscheinlichkeit, erwartetem Wert und Ergebniswahrscheinlichkeit und in der Erweiterung, wie tatsächliche Renditen in Abhängigkeit von den Wettquoten variieren können. Für Kelly-Befürworter denke ich, dass diese Methode effektiver ist als der Einheitseinfluss-Einsatz und sicherlich effektiver als Einheitsverlust und einheitlicher Gewinn.