En este artículo, conocerá la reinterpretación de los diferentes planes de apuestas con la fórmula de Kelly, así como explicaciones sobre el impacto en la pérdida y/o ganancia de unidades, la asimetría de los rendimientos y la simetría de la probabilidad.

Hace cuatro años, se publicó un artículo en la revista "Economics of Sport" sobre cómo debe apostar un apostante rentable en condiciones en las que no se dispone de estimaciones de las verdaderas probabilidades de pago.

Es discutible que un apostante que desee tener una rentabilidad constante a largo plazo deba siquiera ser activo en tales condiciones, pero resulta que muchos apostantes deportivos reconocen que son incapaces de estimarlas con precisión.

No obstante, su estudio es interesante porque muestra cómo los distintos planes de apuestas pueden reinterpretarse como variantes del criterio de Kelly. En este artículo, quiero resumir sus esfuerzos y examinar si lo que descubrieron puede mejorarse.

Reinterpretación de diferentes planes de apuestas con la fórmula de Kelly

Quizá no haya tema más popular en el mundo de la gestión del dinero en las apuestas deportivas que el uso del criterio de Kelly como método de apuesta. En concreto, he demostrado que para una apuesta Kelly simple, en la que sólo se realiza una apuesta a la vez antes de la liquidación, la estrategia es capaz de tener en cuenta los riesgos asociados a no conocer con precisión su ventaja apuesta a apuesta, siempre y cuando se acierte de media.

Pérdida por unidad

La primera de estas estrategias es la pérdida por unidad, o método de apuestas niveladas, en el que el apostante arriesga la misma cantidad en cada apuesta, independientemente de la cuota. Cuanto mayor sea la cuota, mayor será el impacto en el bankroll si la apuesta resulta ganadora, pero menor será la probabilidad de que la apuesta resulte ganadora.

Podemos pensar en las apuestas de pérdida unitaria como un plan Kelly en el que el valor o rendimiento esperado es linealmente proporcional a las probabilidades. Dado que el tamaño de la apuesta Kelly viene dado por EV / cuota - 1 (donde EV es el valor esperado, considerándose rentable todo lo que sea superior a 0), un plan de pérdidas unitarias implica que esta proporción permanece constante.

Por ejemplo, supongamos que el EV es del 10% (0,1) y la cuota es de 2,00. La apuesta sería de 0,1. La apuesta sería de 0,1. Si las cuotas aumentan a 4,00, significa que el EV debe aumentar al 30% (0,3) para que la apuesta se mantenga en 0,1. Una cuota de 101,00 implicaría un EV de 10 o 1.000%, lo que parece poco realista. Esto implicaría unas cuotas reales de sólo 9,18. Ciertamente, ninguna casa de apuestas cometería un error tan grave.

De hecho, en el límite en el que las cuotas tienden a infinito, las cuotas reales tenderían hacia un valor máximo dado por 1 / apuesta, en este caso 10. Una de las principales críticas que se hacen a la apuesta por unidad de pérdida es que supone un riesgo demasiado elevado para las apuestas a largo plazo con bajas probabilidades de ganar. Para los defensores del criterio de Kelly, esto sólo tendría sentido si el EV aumentara realmente en proporción a las cuotas, lo que, como vemos, es poco creíble.

Ganancia unitaria

El segundo plan de gestión del dinero generalmente utilizado por los apostantes es la apuesta unitaria. En este caso, la apuesta es tal que el apostante pretende obtener el mismo beneficio sea cual sea la cuota. Si el objetivo de ganancia, o beneficio, es de 100 euros, las cuotas de 2,00 requerirán una apuesta de 100 euros, mientras que las cuotas de 5,00 requerirán una apuesta de 25 euros. El tamaño de la apuesta es proporcional al recíproco de las probabilidades - 1. En términos de Kelly, la estrategia de ganancia unitaria implica que el EV está completamente desvinculado del criterio de Kelly; todos los EV son iguales sean cuales sean las probabilidades.

En lo que respecta a las apuestas de pérdida unitaria, hay algo que no cuadra. ¿Es posible que la ventaja de un apostante sea la misma si la cuota es 1,11 o 111,00? Las lecciones aprendidas de la varianza sugieren que esto no es muy realista. De hecho, si su EV para probabilidades de 111,00 es del 20% (0,2), el mismo EV para probabilidades de 1,11 implicaría que las probabilidades reales son inferiores a 1, lo que es un completo disparate. Algo no puede tener una probabilidad de resultado superior al 100%.

Impacto unitario

Los autores han propuesto un plan de apuestas alternativo: el impacto unitario, partiendo del supuesto de que este plan se ajusta mejor al método de apuestas Kelly. El método de impacto unitario mantiene constante la diferencia de bankroll entre ganar y perder, independientemente de la longitud o brevedad de las probabilidades.

La apuesta de impacto unitario es proporcional al recíproco de las probabilidades, a diferencia de la ganancia unitaria, que es el recíproco de las probabilidades - 1. Así, si la apuesta es de 100 euros para una cuota de 2,00, la apuesta unitaria de impacto para una cuota de 5,00 será de 40 euros. En cada caso, la diferencia entre la ganancia y la pérdida es de 200 euros (+100 euros/100 euros en el primer caso y +160 euros/40 euros en el segundo).

Para las apuestas de impacto unitario, el EV es proporcional a la cuota - 1 / cuota. Esto significa que el EV aumenta a medida que aumenta la cuota, pero a un ritmo que disminuye hacia un límite, ya que esta relación tiende rápidamente hacia 1. Por ejemplo, si EV = 0,1 para una cuota de 2,00, el límite de EV será 0,2. Aunque este escenario no es tan extremo como en el caso de las apuestas de victoria unitaria, en las que el EV permanece invariable, de nuevo parece subestimar la posibilidad de EVs más elevados para cuotas más largas.

Los pronosticadores de carreras de caballos con éxito suelen obtener rendimientos muy superiores al doble de los que se centran en el hándicap asiático o en el mercado de la diferencia de puntos, aunque esto no significa necesariamente que sean más hábiles (o que tengan más suerte); simplemente tienen más varianza de su lado.

Siguiendo el ejemplo del autor, la tabla siguiente ilustra cómo varía el EV con las cuotas para los tres planes de apuestas diferentes, suponiendo EV = 3% para cuotas = 2,00 para cada uno.

Como ya se ha comentado, tanto la apuesta "unidad de pérdida" como la "unidad de ganancia" parecen implicar relaciones poco realistas entre las cuotas y el VE.

Los autores han analizado la base de datos de pronósticos de un conocido sitio de pronósticos y creen haber confirmado que la relación entre el VE y las cuotas implícitas en la apuesta de impacto unitario refleja mejor los beneficios observados y esperados de los pronosticadores (estos últimos se basan en los precios de cierre). Yo sigo sin estar convencido. Repito, el método de impacto unitario sólo producirá un VE que, como mucho, sea el doble del VE para cuotas = 2,00. ¿Hay alguna alternativa mejor?

Revisión de la distribución T

Hace tres años, presenté el uso de la distribución T para evaluar pronosticadores y distinguir la suerte de la habilidad. Similar a la distribución normal (y utilizada en su lugar cuando sólo conocemos la desviación típica de la muestra y no la de la población), permite determinar el grado de improbabilidad de una muestra dada suponiendo que se conoce la media de la población.

He utilizado mucho la distribución T en mi trabajo para ayudar a los apostantes a calcular la probabilidad de que sus resultados sean fruto del azar, suponiendo que no tienen ninguna habilidad. Cuanto menor sea la probabilidad, mayor será la confianza subjetiva en que el azar no tiene nada que ver con los beneficios de las apuestas.

En el centro de esta prueba está el estadístico t o puntuación t, a partir del cual se pueden derivar las probabilidades. He demostrado que para una apuesta de pérdida unitaria, y cuando las probabilidades de su récord no varían demasiado, esta estadística se puede aproximar con la siguiente fórmula.

donde n es el número de apuestas, o es la cuota media y r es el rendimiento de la inversión o rendimiento + 1.

Al igual que la puntuación z, con la que los handicappers están más familiarizados, es esencialmente una medida del número de desviaciones estándar que su rendimiento se desvía de una media esperada de cero, si apuesta sin habilidad y a cuotas justas. Una puntuación t de 2, por ejemplo, significa que sólo se espera una rentabilidad mejor que la de su récord el 2,5% de las veces, suponiendo que no tiene ninguna habilidad. La puntuación t es, por tanto, un tipo de medida de probabilidad. Cuanto más alta es la puntuación t, menos probable es la observación. Utilicémoslo para determinar la probabilidad de diferentes EVs (suponiendo que no hay habilidad) en función de las probabilidades que estamos apostando.

Rendimientos asimétricos

Supongamos que apuesta por un equipo con un 80% de probabilidades de ganar, con una cuota de 1,25. Supongamos ahora que el corredor de apuestas piensa erróneamente que la probabilidad de ganar es del 75%. Está de promoción y no tiene margen. Su cuota es de 1,333. Por lo tanto, su VE es del 6,667% (1,333/1,25 - 1 ó 0,80/0,75 - 1).

Consideremos ahora un segundo escenario: la probabilidad real es del 20% (cuota justa de 5,00), pero la casa de apuestas considera que es del 15% (cuota publicada de 6,667). En este caso, su EV es del 33,33% (6,667/5,00 - 1 o 0,20/0,15 - 1). La diferencia en la ganancia porcentual esperada entre su estimación y la de la casa de apuestas es la misma, pero el VE es 5 veces mayor. Parece que, en términos de EV, cuanto mayor es la cuota, mayor es la penalización por errores equivalentes. Pero, ¿cuál es la probabilidad de estos errores?

La simetría de la probabilidad

Volvamos a escribir la fórmula de la puntuación t anterior (suponiendo que todas nuestras apuestas tienen la misma cuota, o). Como sabemos que r = q / p, donde p es la probabilidad implícita de las cuotas de la casa de apuestas (es decir, 1/o) y q es su probabilidad estimada (que es "verdadera" si su modelo de predicción es preciso), podemos demostrar que :

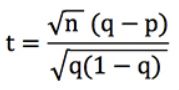
Supongamos que n, nuestro número de apuestas, es igual a 100. Para q = 0,8 y p = 0,75, t = 1,25. Del mismo modo, para q = 0,2 y p = 0,15, t = 1,25 también. Suponiendo que el corredor de apuestas, y no nuestro modelo, sea realmente correcto, dicha puntuación t correspondería a una probabilidad de resultado del 10,7% (utilizando la función =TDIST de Excel).

En 100 apuestas, deberíamos obtener una rentabilidad superior al 6,667% a cuotas de 1,333, o superior al 33,33% a cuotas de 6,667, o el 10,7% de las veces. Los beneficios más altos a cuotas más altas son tan probables como los beneficios más bajos a cuotas más cortas, por lo que los pronosticadores de carreras tienen la ilusión de que son mejores que los handicappers, o peores si pierden.

He intentado ilustrar esta simetría de probabilidades utilizando las siguientes tablas. Los valores son extremos simplemente para ilustrar el punto; obviamente ningún apostador será capaz de hacer esto bien, o mal, para la mayoría de los escenarios.

La primera muestra la asimetría del EV para diferentes pares p, q. La segunda muestra la simetría de las puntuaciones t. La segunda muestra la simetría de las puntuaciones t. He mostrado las puntuaciones t absolutas (eliminando el signo negativo para los EV negativos cuando q < p) para mayor claridad. No sólo es tan probable un par p, q de 0,3/0,7 como un par 0,7/0,3, sino que también lo son pares como 0,7/0,5 y 0,3/0,1, 0,8/0,7 y 0,2/0,1 por las razones descritas anteriormente.

Una nueva función de cuota EV

Para una cuota y un EV dados, existe una probabilidad t (que se duplica cuando el número de apuestas se multiplica por 4). Podemos reordenar la fórmula de la puntuación t para expresarla en términos de r. Esto conduce a una cuadrática bastante horrible con una solución aún más horrible.

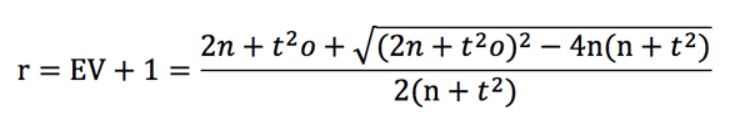
Se trata de una solución mucho más desagradable que odds - 1 / odds, pero representémosla de todos modos para el escenario en el que EV = 0,03 y odds = 2,00. Este gráfico se muestra a continuación, junto con las funciones EV anteriores para la pérdida unitaria, la ganancia unitaria y el impacto unitario de la apuesta.

Aunque la función puede ser difícil de escribir, es más intuitiva porque interpreta los beneficios esperados en términos de probabilidad estadística. Para las apuestas de impacto unitario, el EV nunca puede ser superior al 6% cuando es del 3% para cuotas de 2,00. Pero con mi función, puede crecer indefinidamente, aunque no tan irrealmente rápido como para las apuestas de impacto unitario, pero en línea con lo que predice la varianza estadística. Para cuotas de 10 es del 9,4%, para cuotas de 50 es del 23,3% y para cuotas de 1.000 es del 150%.

Una crítica obvia es que esta función, basada en la puntuación T, asume que el apostante no tiene habilidad. Simplemente expresa la probabilidad de que ocurran cosas suponiendo que no hay habilidad. Pero esto es una interpretación errónea; incluso en presencia de habilidad, se aplican las mismas leyes estadísticas asociadas a la varianza.

La posición de la curva naranja cambiaría, pero la forma seguiría siendo la misma. A continuación he ilustrado algunas trayectorias posibles para apostadores con distintos grados de suerte o habilidad, dependiendo del término utilizado. La curva inicial para el jugador con un EV del 3% a una cuota de 2,00 se muestra siempre en naranja.

Otra crítica podría ser que también asumimos que cualquier habilidad es independiente de las probabilidades, es decir, que es la misma independientemente de las probabilidades. Dadas las ineficiencias del mercado, como el sesgo a largo plazo, esta suposición puede no ser adecuada.

Comprobación de la función

¿Podemos probar la validez de esta nueva función EV? Mi sistema de apuestas Wisdom of the Crowd, con el que estarán familiarizados quienes me sigan regularmente en Twitter y en Football-Data, utiliza las cuotas más eficientes de Pinnacle para estimar el EV disponible en las cuotas de otras casas de apuestas.

Utilizando una muestra de datos de cuotas de partidos de ligas domésticas europeas que se remontan a la temporada 2012/13, encontré 55.237 ocasiones en las que había disponible un EV rentable (>0). La media fue del 2,20% (para que conste, el rendimiento real de las apuestas de pérdida unitaria fue del 1,77%, bien dentro de los márgenes estadísticos de error del modelo), con cuotas medias de 3,30. Con estas cifras, podemos utilizar mi fórmula de solución cuadrática para construir una curva de función EV como las anteriores. Ésta es la curva naranja que aparece a continuación.

Compare esta curva con los EVs del modelo real calculados sobre la base de las expectativas de pago del 1% (mostradas como probabilidades en el gráfico) y con la curva de la función EV- predicha por la apuesta de impacto unitario. Aunque la coincidencia no es perfecta, la función EV t-score es probablemente un mejor predictor de los EVs aproximados basados en las probabilidades de apuestas.

Un razonamiento

Los más observadores entre ustedes podrían estar pensando ahora: ¿qué sentido tiene utilizar una función EV para predecir el EV para diferentes cuotas cuando su modelo Wisdom of the Crowd lo hace explícitamente para cada apuesta? En efecto, se trata de una opinión válida, por lo que gran parte de este artículo podría considerarse más bien teórico.

No obstante, incluso los modelos precisos (por término medio) tienen incertidumbre epistémica para cada apuesta. Además, la incertidumbre aleatoria (o inherente) hace prácticamente imposible evaluar la verdadera probabilidad de ganar.

Por lo tanto, el objetivo de este ejercicio, al igual que el de los autores, era ilustrar cómo se puede intentar aproximar el EV cuando se reconocen estas incertidumbres cuantitativas, cuando el modelo de predicción no estima explícitamente las probabilidades de ganar o cuando el método de predicción es más cualitativo y se basa más en la intuición que en el análisis de datos. Si conoce sus probabilidades, este método le permitirá estimar su EV; si conoce su EV, podrá determinar la apuesta Kelly que debe utilizar.

Esta metodología de puntuación t puede ser enrevesada, pero sus resultados se derivan de un razonamiento más intuitivo de la relación entre la probabilidad de ganar, el valor esperado y la probabilidad de resultado y, por extensión, de cómo puede verse que los beneficios reales varían con las cuotas de las apuestas. Para los seguidores de Kelly, creo que este método es más eficaz que la apuesta de impacto unitario, y desde luego más eficaz que la pérdida unitaria y la ganancia unitaria.