La Loi de Poisson appliquée aux Paris Sportifs

La loi de Poisson est un outil statistique puissant utilisé pour prédire la probabilité de divers résultats dans des événements rares, comme les scores exacts dans les paris sportifs. Dans cet article, nous explorerons comment la loi de Poisson peut être appliquée aux paris sportifs, en détaillant sa définition, ses formules, des exemples concrets, et en abordant ses limites.

Définition de la Loi de Poisson

La loi de Poisson est une distribution de probabilité qui décrit le nombre de fois qu'un événement se produit dans un intervalle de temps ou d'espace fixe. Elle est particulièrement utile pour modéliser des événements rares ou des occurrences aléatoires.

Formule de la Loi de Poisson

La formule de la loi de Poisson est la suivante :

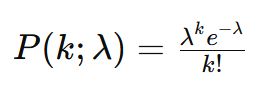
où :

   P(k;λ) est la probabilité d'observer kk événements dans un intervalle donné.

   λ est le taux moyen d'occurrence des événements.

   k est le nombre d'événements observés.

   e est la base du logarithme naturel (environ égale à 2,71828).

Exemples de Prédictions de Scores Exacts avec, un premier exemple fictif entre une équipe A et une équipe B, puis un exemple réel entre Lille et Lens en Ligue 1 (2023/24)

Exemple 1 : Match entre l'Équipe A et l'Équipe B

Supposons que l'Équipe A marque en moyenne 1,5 buts par match et que l'Équipe B marque en moyenne 1,2 buts par match. Pour prédire les scores exacts, nous calculons les probabilités pour chaque score possible.

Calcul des Probabilités des Scores

Pour l'Équipe A :

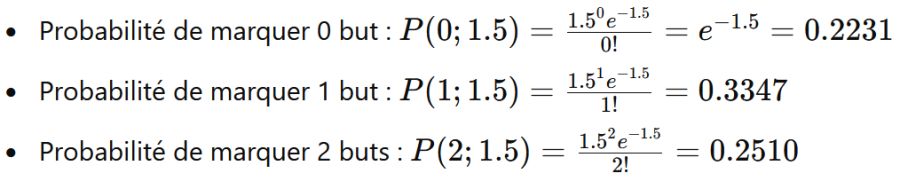
Pour l'Équipe B :

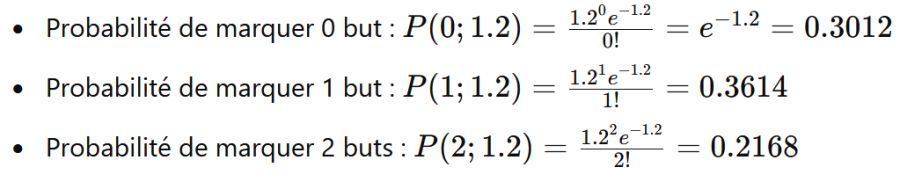
Pour trouver la probabilité d'un score exact, nous multiplions les probabilités correspondantes de chaque équipe.

Par exemple, pour un score de 2-1 en faveur de l'Équipe A :

   P(Score 2-1)=P(2;1.5)×P(1;1.2)=0.2510×0.3614=0.0907P(Score 2-1)=P(2;1.5)×P(1;1.2)=0.2510×0.3614=0.0907

Calculer la Force de l'Attaque et le Potentiel de la Défense

Pour une analyse plus approfondie, nous devons calculer la force de l'attaque (λA​) et le potentiel de la défense (λB) pour chaque équipe. Cela peut être fait en utilisant les données historiques des performances offensives et défensives de chaque équipe.

Calcul de la Force de l'Attaque (λA​) et de la Défense (λB)

En utilisant la loi de Poisson, nous pouvons prédire plusieurs résultats pour différents matchs en calculant les probabilités pour chaque score possible. Ces prédictions peuvent ensuite être utilisées pour orienter les paris sportifs.

Convertir la Probabilité Estimée en Cotes

Les probabilités estimées peuvent être converties en cotes de paris en utilisant la formule suivante :

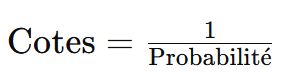
Par exemple, si la probabilité estimée d'un score exact est de 0,0907, les cotes seront :

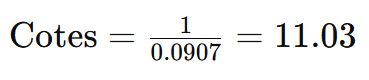
Exemple 2 : Match entre Lille et Lens en Ligue 1 lors de la saison 2023/2024

Pour appliquer la loi de Poisson au match Lille (domicile) contre Lens (extérieur) de la saison 2023/2024, nous allons utiliser les statistiques des deux équipes.

Voici les étapes pour effectuer cette analyse :

Étape 1 : Collecte des Données

Statistiques de Lille

   Moyenne de buts marqués par match à domicile : 1,89

   Moyenne de buts encaissés par match à domicile : 0,89

Statistiques de Lens

   Moyenne de buts marqués par match à l'extérieur : 0,91

   Moyenne de buts encaissés par match à l'extérieur : 1,00

Étape 2 : Calcul de la Force de l'Attaque et du Potentiel de la Défense

Pour Lille :

   Force de l'attaque (λA​) = 1,89

   Potentiel de la défense (λB​) = 0,89

Pour Lens :

   Force de l'attaque (λA​) = 0,91

   Potentiel de la défense (λB) = 1,00

Étape 3 : Application de la Loi de Poisson

Calcul des Probabilités des Scores

Nous utilisons la formule de la loi de Poisson pour calculer les probabilités des différents scores.

Pour Lille marquant k buts :

Pour Lens marquant k buts :

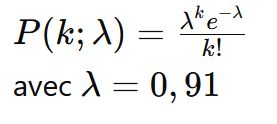
Pour Lens marquant k buts :

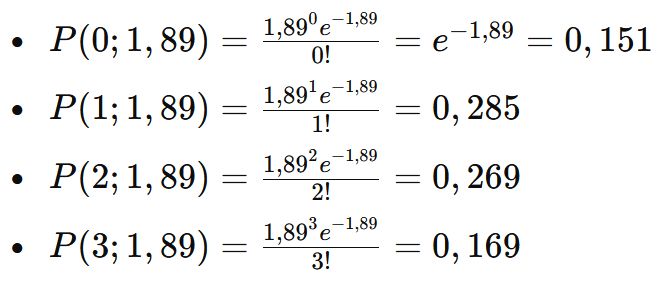
Calcul des Probabilités des Scores pour Lens

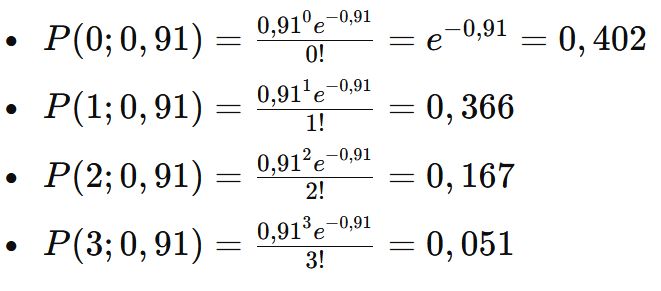
Étape 4 : Calcul des Scores Probables

Pour obtenir la probabilité combinée d'un score exact, nous multiplions les probabilités correspondantes de chaque équipe. Par exemple :

Probabilité d'un score de 2-1 en faveur de Lille :

Étape 5 : Conversion des Probabilités en Cotes

Pour convertir ces probabilités en cotes, nous utilisons la formule suivante :

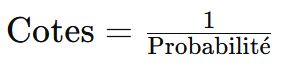
Pour un score de 2-1 pour Lille :

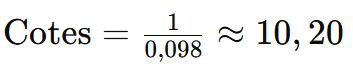
Les Limites de la Loi de Poisson

Malgré son utilité, la loi de Poisson présente certaines limites :

   Elle suppose que les événements sont indépendants, ce qui n'est pas toujours le cas dans les matchs de football.

   Elle ne prend pas en compte les facteurs contextuels tels que les blessures, les conditions météorologiques, ou les changements tactiques.

   Elle est basée sur des moyennes historiques et peut ne pas refléter les performances actuelles des équipes.

Conclusion

La loi de Poisson est un outil puissant pour prédire les scores exacts dans les paris sportifs, en fournissant une base mathématique pour estimer les probabilités de divers résultats. Cependant, il est essentiel de reconnaître ses limites et de l'utiliser en complément d'autres analyses pour obtenir des prédictions plus précises et fiables. En combinant la loi de Poisson avec une compréhension approfondie des équipes et des circonstances du match, les parieurs peuvent améliorer leurs stratégies et augmenter leurs chances de succès.