In questo articolo, imparerete la reinterpretazione dei vari piani di scommessa con la formula di Kelly, nonché le spiegazioni sull'impatto sulla perdita e/o guadagno di unità, l'asimmetria dei rendimenti e la simmetria della probabilità.

Quattro anni fa, è stato pubblicato un articolo sul giornale "Economia dello Sport" su come un scommettitore redditizio dovrebbe scommettere in condizioni in cui le stime delle reali probabilità di vincita non sono disponibili.

La questione se un scommettitore desideroso di avere una redditività costante a lungo termine dovrebbe anche essere attivo in tali condizioni è discutibile, ma risulta che molti scommettitori sportivi riconoscono di non essere in grado di stimarle con precisione.

Tuttavia, il loro studio è interessante in quanto mostra come diversi piani di scommessa possano essere reinterpretati come varianti del criterio di Kelly. In questo articolo, desidero riassumere i loro sforzi ed esaminare se ciò che hanno scoperto possa essere migliorato.

Reinterpretare i vari piani di scommessa con la formula di Kelly

Non c'è forse argomento più popolare nel mondo della gestione del denaro delle scommesse sportive che l'uso del criterio di Kelly come metodo di scommessa. Ho dimostrato, in particolare, che per una semplice scommessa Kelly, in cui viene piazzata una sola scommessa alla volta prima della risoluzione, la strategia è in grado di tenere conto dei rischi legati al fatto di non conoscere precisamente il proprio vantaggio basato su una scommessa alla volta, finché si è precisi in media.

Perdita unitaria

La prima di queste strategie è la perdita unitaria, o metodo degli importi costanti, secondo la quale lo scommettitore rischia la stessa puntata su ogni scommessa, indipendentemente dalla quota. Più alta è la quota, maggiore è l'impatto sul bankroll in caso di vincita, ma minore è la probabilità che la scommessa risulti vincente.

Possiamo considerare la scommessa sulle perdite unitarie come un piano Kelly in cui il valore atteso o rendimento è linearmente proporzionale alla quota. Dato che la dimensione della scommessa Kelly è data da VE / quota - 1 (dove VE è il valore atteso, tutto ciò che è superiore a 0 è considerato redditizio), un piano di perdita unitaria implica che questo rapporto rimanga costante.

Ad esempio, supponiamo che la VE sia del 10% (0,1) e la quota sia di 2,00. La puntata sarebbe di 0,1. Se la quota sale a 4,00, significa che la VE deve salire al 30% (0,3) affinché la puntata rimanga a 0,1. Una quota di 101,00 implicherebbe una VE di 10 o 1.000%, il che sembra un po' irrealistico. Questo implicherebbe una quota reale di soli 9,18. È certo che nessun bookmaker commetterà un errore così grave.

Infatti, nel limite in cui le quote tendono all'infinito, le quote reali tenderebbero a un valore massimo dato da 1 / puntata, in questo caso 10. Una delle principali critiche mosse contro la scommessa sulle perdite unitarie è che comporta un rischio troppo elevato per le scommesse a lungo termine con basse probabilità di vincita. Per i sostenitori del criterio di Kelly, ciò avrebbe senso solo se la VE aumentasse realmente in modo proporzionale alla quota, il che, come possiamo vedere, è difficilmente credibile.

Guadagno unitario

Il secondo piano di gestione del denaro generalmente utilizzato dagli scommettitori è la scommessa all'unità. In questo caso, la puntata è tale che lo scommettitore mira a ottenere lo stesso profitto indipendentemente dalla quota. Se l'obiettivo di guadagno, o profitto, è di 100 €, una quota di 2,00 richiederà una puntata di 100 €, mentre una quota di 5,00 richiederà una puntata di 25 €. La dimensione della puntata è proporzionale al reciproco della quota - 1. In termini di Kelly, la strategia di guadagno unitario implica che la VE non è assolutamente correlata con il criterio di Kelly; tutte le VE sono le stesse indipendentemente dalle quote.

Per quanto riguarda le scommesse sulle perdite unitarie, c'è qualcosa che non va. È possibile che il vantaggio di uno scommettitore sia lo stesso, sia che la quota sia 1,11 sia che sia 111,00? Le lezioni apprese dalla varianza suggeriscono che ciò non è molto realistico. Infatti, se la vostra VE per una quota di 111,00 è del 20% (0,2), la stessa VE per una quota di 1,11 implicherebbe che la vera quota sia inferiore a 1, il che è del tutto assurdo. Qualcosa non può avere una probabilità di risultato superiore al 100%.

Impatto unitario

Gli autori hanno proposto un piano di scommessa alternativo: l'impatto unitario, ipotizzando che questo piano si adatti meglio al metodo di scommessa di Kelly. Il metodo dell'impatto unitario mantiene costante la differenza di bankroll tra vincere e perdere, indipendentemente dalla lunghezza o brevità delle quote.

La puntata dell'impatto unitario è proporzionale al reciproco della quota, a differenza del guadagno unitario che è il reciproco della quota - 1. Così, se la puntata è di 100 € per una quota di 2,00, la puntata di impatto unitario per una quota di 5,00 sarà di 40 €. In ogni caso, la differenza tra il guadagno e la perdita è di 200 € (+100 €/100 € nel primo caso e +160 €/40 € nel secondo).

Per le scommesse a impatto unitario, la VE è proporzionale alla quota - 1 / quota. Ciò significa che la VE aumenta con l'aumento delle quote, ma a un tasso decrescente verso un limite, poiché questo rapporto tende rapidamente verso 1. Ad esempio, se la VE = 0,1 per una quota di 2,00, il limite della VE sarà di 0,2. Anche se questo scenario non è così estremo come per la scommessa sui guadagni unitarie, dove la VE rimane invariata, sembra nuovamente sottovalutare la possibilità di VE più elevate per quote più lunghe.

I pronosticatori di corse di cavalli di successo hanno generalmente rendimenti notevolmente superiori al doppio di quelli che si concentrano sul mercato degli handicap asiatici o delle scommesse con spread, anche se ciò non significa necessariamente che siano più competenti (o più fortunati); hanno semplicemente una maggiore varianza dalla loro parte.

Seguendo le indicazioni dell'autore, la tabella sottostante illustra come la VE varia in base alle quote per i tre diversi piani di scommessa, assumendo che la VE = 3% per quote = 2,00 per ciascuno di essi.

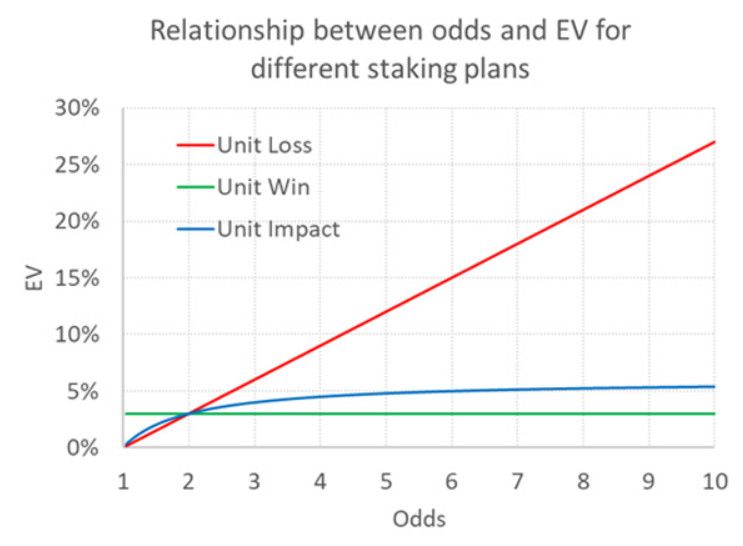
Come abbiamo visto in precedenza, i piani di scommessa "perdita unitaria" e "guadagno unitario" sembrano entrambi implicare relazioni irrealistiche tra le quote e la VE.

Gli autori hanno analizzato il database delle scelte di scommesse di un noto sito di pronostici e ritengono di aver confermato che la relazione tra VE e quota implicata dalla scommessa sull'impatto unitario riflette meglio i rendimenti osservati e attesi dei pronosticatori (questi ultimi basati sui prezzi di chiusura). Non sono ancora convinto. Ripeto, il metodo dell'impatto unitario non produrrà mai una VE che è al massimo il doppio della VE per quote = 2,00. Esiste un'alternativa migliore?

Riesame della distribuzione T

Tre anni fa, ho presentato l'uso della distribuzione T per valutare i pronosticatori e distinguere la fortuna dall'abilità. Simile alla distribuzione normale (e usata al suo posto quando si conosce solo la deviazione standard del campione e non quella della popolazione), permette di determinare il grado di improbabilità di un campione dato supponendo che la media della popolazione sia nota.

Ho usato molto la distribuzione T nel mio lavoro per aiutare gli scommettitori a determinare la probabilità che i loro risultati siano frutto del caso, supponendo che non abbiano competenze. Più bassa è la probabilità, più si può essere soggettivamente sicuri che il caso non ha nulla a che fare con i profitti delle scommesse.

Al centro di questo test c'è la statistica t o il punteggio t, da cui possono essere derivate le probabilità. Ho dimostrato che per una scommessa a perdita unitaria, e quando le quote del vostro

 record non variano troppo, questa statistica può essere approssimata con la seguente formula.

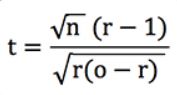
dove n è il numero di scommesse, o la quota media e r il ritorno sull'investimento o rendimento + 1.

Come il punteggio z, che i bookmaker potrebbero conoscere meglio, è essenzialmente una misura del numero di deviazioni standard che il vostro rendimento si discosta da una media attesa di zero, se scommettete senza competenze e a quote equi. Un punteggio t di 2, ad esempio, significa che un rendimento migliore di quello ottenuto dal vostro record è atteso solo il 2,5% delle volte, supponendo che non abbiate competenze. Il punteggio t è quindi un tipo di misura della probabilità. Più alto è il punteggio t, meno probabile è l'osservazione. Usiamolo per determinare la probabilità di diverse VE (supponendo che non ci siano competenze) in base alle quote su cui scommettiamo.

L'asimmetria dei rendimenti

Supponiamo che scommettiate su una squadra con l'80% di probabilità di vincere, con una quota di 1,25. Supponiamo ora che il bookmaker pensi erroneamente che la probabilità di vittoria sia del 75%. Fa una promozione e non ha margine. La sua quota è di 1,333. Pertanto, la vostra VE è del 6,667% (1,333/1,25 - 1 o 0,80/0,75 - 1).

Consideriamo ora un secondo scenario: la reale probabilità è del 20% (quota equa di 5,00), ma il bookmaker stima che sia del 15% (quota pubblicata di 6,667). Questa volta, la vostra VE è del 33,33% (6,667/5,00 - 1 o 0,20/0,15 - 1). La differenza di percentuale di guadagno atteso tra la vostra stima e quella del bookmaker è la stessa, ma la VE è 5 volte maggiore. Sembra che in termini di VE, gli errori equivalenti siano tanto più penalizzati quanto più alte sono le quote. Ma qual è la probabilità di questi errori?

La simmetria della probabilità

Riscriviamo la formula del punteggio t sopra (supponendo che tutte le nostre scommesse abbiano la stessa quota, o). Poiché sappiamo che r = q / p, dove p è la probabilità implicita della quota del bookmaker (cioè 1/o) e q è la vostra probabilità stimata (che è "vera" se il vostro modello di previsione è preciso), si può dimostrare che:

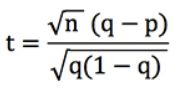
Supponiamo che n, il nostro numero di scommesse, sia pari a 100. Per q = 0,8 e p = 0,75, t = 1,25. Allo stesso modo, per q = 0,2 e p = 0,15, t = 1,25 anche. Supponendo che il bookmaker, e non il nostro modello, sia effettivamente corretto, un tale punteggio t corrisponderebbe a una probabilità di risultato del 10,7% (utilizzando la funzione =TDIST di Excel).

Su 100 scommesse, dovremmo ottenere un rendimento superiore al 6,667% per una quota di 1,333, o superiore al 33,33% per una quota di 6,667, il 10,7% delle volte. Rendimenti maggiori a quote più alte sono altrettanto probabili di rendimenti inferiori a quote più basse; ecco perché i pronosticatori di corse hanno l'illusione di essere migliori dei bookmaker, o peggio se sono perdenti.

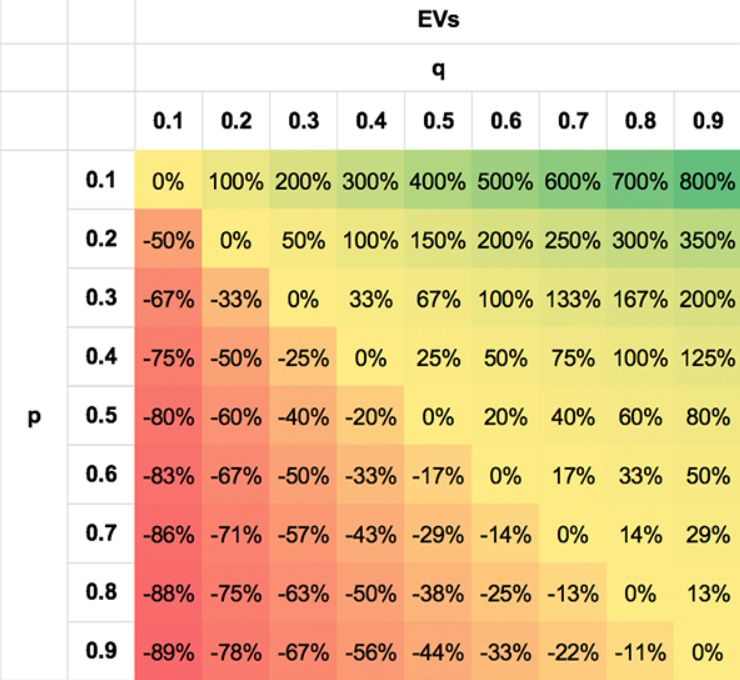
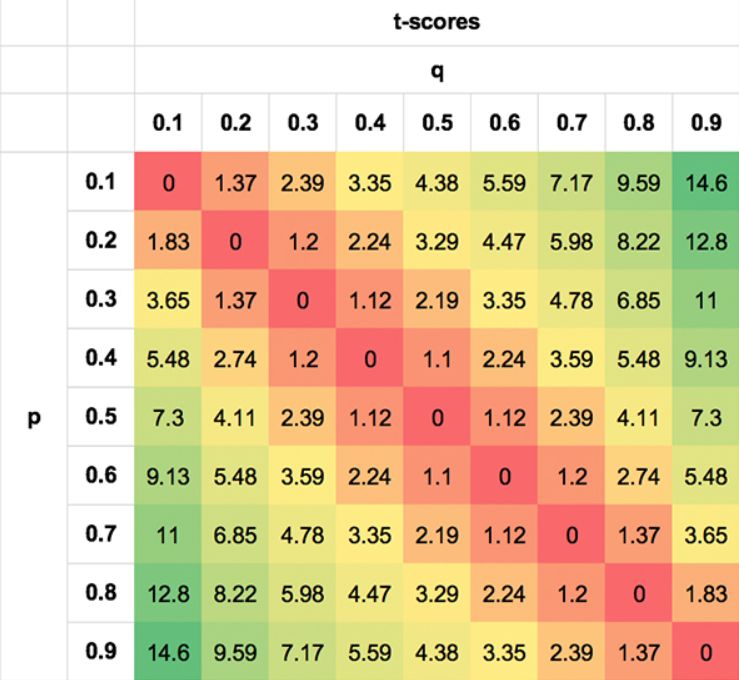
Ho tentato di illustrare questa simmetria delle probabilità con le seguenti tabelle. I valori sono estremi semplicemente per illustrare il punto; è ovvio che nessuno scommettitore sarà in grado di fare così bene, o così male, nella maggior parte degli scenari.

La prima mostra l'asimmetria della VE per diverse coppie p, q. La seconda mostra la simmetria dei punteggi t. La seconda mostra la simmetria dei punteggi t. Ho indicato i punteggi t assoluti (rimuovendo il segno negativo per le VE negative quando q < p) per maggiore chiarezza. Non solo una coppia p, q di 0,3/0,7 è altrettanto probabile di una coppia 0,7/0,3, ma lo stesso vale per coppie come 0,7/0,5 e 0,3/0,1, 0,8/0,7 e 0,2/0,1 per i motivi sopra descritti.

Una nuova funzione di quota VE

Per una quota e una VE date, esiste una probabilità t (che raddoppia quando il numero di scommesse è moltiplicato per 4). Possiamo riorganizzare la formula del punteggio t per esprimerla in termini di r. Ciò porta a una quadratica piuttosto orribile con una soluzione ancora più orribile.

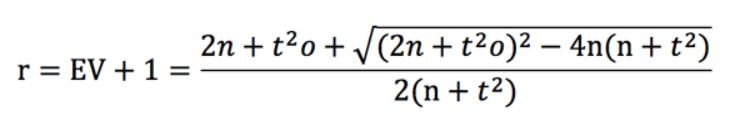
È una soluzione molto più spiacevole di quota - 1 / quota, ma rappresentiamola comunque per lo scenario in cui VE = 0,03 e quota = 2,00. Questo grafico è presentato di seguito, insieme alle precedenti funzioni VE per la perdita unitaria, il guadagno unitario e l'impatto unitario della scommessa.

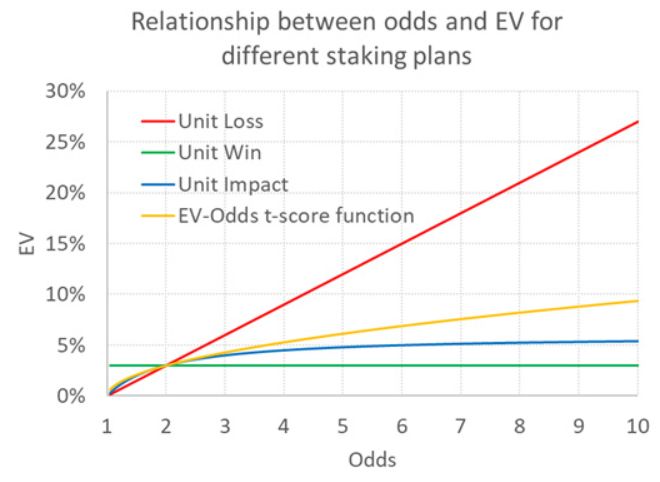
Sebbene la funzione possa essere difficile da scrivere, è più intuitiva poiché interpreta i rendimenti attesi in termini di probabilità statistica. Per le scommesse a impatto unitario, la VE non può mai essere superiore al 6% quando è del 3% per quote di 2,00. Ma con la mia funzione, può crescere indefinitamente, anche se non a una velocità irrealistica come per le scommesse sulle perdite unitarie, ma in conformità con quanto predetto dalla varianza statistica. Per quote di 10, è del 9,4%, per quote di 50, è del 23,3% e per quote di 1.000, è del 150%.

Una critica ovvia è che questa funzione, basata sul punteggio T, presume che lo scommettitore non abbia competenze. Esprime semplicemente la probabilità che le cose accadano supponendo che non ci siano competenze. Ma questa è un'interpretazione errata; anche in presenza di competenze, le stesse leggi statistiche associate alla varianza si applicano.

La posizione della curva arancione cambierebbe, ma la forma rimarrebbe la stessa. Ho illustrato di seguito alcune possibili traiettorie per scommettitori con vari gradi di fortuna o abilità, a seconda del termine utilizzato. La curva iniziale dello scommettitore con una VE del 3% per una quota di 2,00 è sempre rappresentata in arancione.

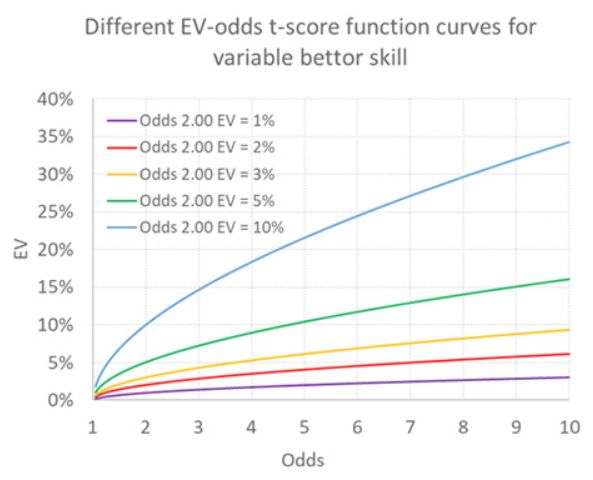
Un'altra critica potrebbe essere che presumiamo anche che qualsiasi competenza sia indipendente dalle quote, cioè che sia la stessa indipendentemente dalle quote. Dato le inefficienze del mercato, come il bias favorito a lungo termine, questa ipotesi potrebbe non essere appropriata.

Test della funzione

Possiamo testare la validità di questa nuova funzione VE? Il mio sistema di scommesse "Wisdom of the Crowd", che coloro che mi seguono regolarmente su Twitter e Football-Data conoscono bene, utilizza le quote più efficaci di Pinnacle per stimare la VE disponibile nelle quote di altri bookmaker.

Da un campione di dati di quote di partite dei campionati nazionali europei risalenti alla stagione 2012/13, ho trovato 55.237 occasioni in cui era disponibile una VE redditizia (>0). La media era del 2,20% (per la cronaca, la performance reale delle puntate a perdita unitaria era dell'1,77%, ben al di sotto dei margini di errore statistici del modello), con quote medie di 3,30. Con questi numeri, possiamo usare la mia formula di soluzione quadratica per costruire una curva di funzione VE come quelle sopra. Questa è la curva arancione qui sotto.

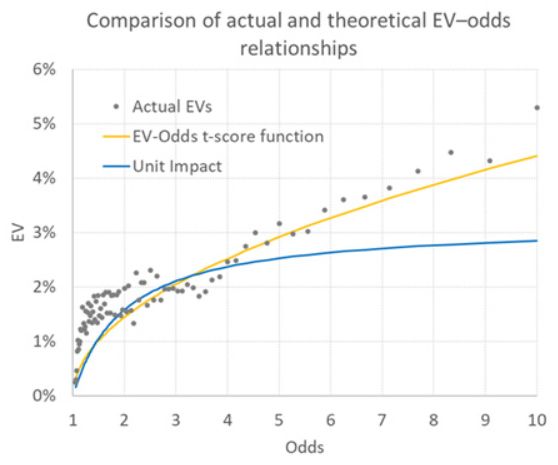
Confrontate questa curva, da un lato, con le VE del modello reale calcolate in base alle aspettative di guadagno dell'1% (indicate sotto forma di quote nel grafico) e, dall'altro, con la curva della funzione VE predetta dalla scommessa a impatto unitario. Sebbene la corrispondenza non sia perfetta, la funzione VE t-score permette forse di prevedere meglio le VE approssimative basate sulle quote delle scommesse.

Un ragionamento

I più osservatori tra voi potrebbero ora chiedersi: qual è il punto di usare una funzione VE per prevedere la VE per diverse quote quando il vostro modello della saggezza della folla lo fa esplicitamente per ogni scommessa? È infatti un giudizio valido, e gran parte

 di questo articolo potrebbe quindi essere considerata piuttosto teorica.

Tuttavia, anche i modelli precisi (in media) presentano un'incertezza epistemica per ogni scommessa. Inoltre, l'incertezza aleatoria (o intrinseca) rende praticamente impossibile la valutazione delle reali probabilità di vincita.

L'obiettivo di questo esercizio, come per gli autori, era quindi di illustrare come si può tentare di stimare approssimativamente la propria VE quando si riconoscono queste incertezze quantitative, quando il modello di previsione non stima esplicitamente le probabilità di vittoria o quando il metodo di previsione è più qualitativo e si basa su intuizioni piuttosto che sull'analisi dei dati. Se conoscete le vostre probabilità, questo metodo vi permetterà di stimare la vostra VE; se conoscete la vostra VE, potrete allora determinare la puntata di Kelly che dovreste utilizzare.

Questa metodologia del punteggio t può essere complicata, ma i suoi risultati sono derivati da un ragionamento più intuitivo della relazione tra la probabilità di vincita, il valore atteso e la probabilità di risultato, e per estensione, come i rendimenti reali possono essere considerati variabili con le quote delle scommesse. Per i sostenitori di Kelly, penso che questo metodo sia più efficace rispetto alla scommessa sull'impatto unitario e sicuramente più efficace rispetto alla perdita unitaria e al guadagno unitario.