The Poisson distribution is a powerful statistical tool used to predict the probability of various outcomes in rare events, such as exact scores in sports betting. In this article, we will explore how the Poisson distribution can be applied to sports betting by detailing its definition, formulas, concrete examples, and discussing its limitations.
Definition of the Poisson Distribution
The Poisson distribution is a probability distribution that describes the number of times an event occurs in a fixed interval of time or space. It is particularly useful for modeling rare events or random occurrences.
Poisson Distribution Formula
The formula for the Poisson distribution is as follows:
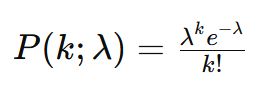
where:
- P(k;λ) is the probability of observing \( k \) events in a given interval.
- λ is the average rate of occurrence of the events.
- k is the number of events observed.
- e is the base of the natural logarithm (approximately equal to 2.71828).
Examples of Exact Score Predictions with a fictitious example between Team A and Team B, and a real example between Lille and Lens in Ligue 1 (2023/24)
Example 1: Match between Team A and Team B
Suppose Team A scores an average of 1.5 goals per match and Team B scores an average of 1.2 goals per match. To predict the exact scores, we calculate the probabilities for each possible score.
Calculating Score Probabilities
For Team A:
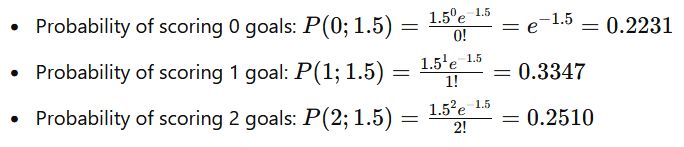
For Team B:
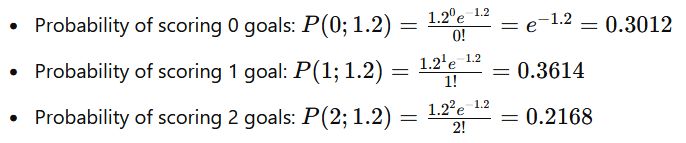
To find the probability of an exact score, we multiply the corresponding probabilities of each team.
For example, for a 2-1 score in favor of Team A:
P(Score 2-1)=P(2;1.5)×P(1;1.2)=0.2510×0.3614=0.0907P(Score 2-1)=P(2;1.5)×P(1;1.2)=0.2510×0.3614=0.0907
Calculating Attack Strength and Defense Potential
For a more in-depth analysis, we need to calculate the attack strength (λA) and defense potential (λB) for each team. This can be done using historical performance data of the teams' offensive and defensive capabilities.
Calculating Attack Strength (λA) and Defense (λB)
Using the Poisson distribution, we can predict several outcomes for different matches by calculating the probabilities for each possible score. These predictions can then be used to guide sports betting.
Converting Estimated Probability to Odds
The estimated probabilities can be converted into betting odds using the following formula:
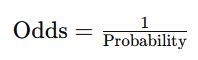
For example, if the estimated probability of an exact score is 0.0907, the odds will be:
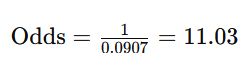
Example 2: Match between Lille and Lens in Ligue 1 during the 2023/2024 Season
To apply the Poisson distribution to the match between Lille (home) and Lens (away) in the 2023/2024 season, we will use the statistics of both teams.
Here are the steps to perform this analysis:
Step 1: Data Collection
Lille Statistics
- Average goals scored per home match: 1.89
- Average goals conceded per home match: 0.89
Lens Statistics
- Average goals scored per away match: 0.91
- Average goals conceded per away match: 1.00
Step 2: Calculating Attack Strength and Defense Potential
For Lille:
- Attack strength (λA) = 1.89
- Defense potential (λB) = 0.89
For Lens:
- Attack strength (λA) = 0.91
- Defense potential (λB) = 1.00
Step 3: Applying the Poisson Distribution
Calculating Score Probabilities
We use the Poisson distribution formula to calculate the probabilities of different scores.
For Lille scoring k goals:
For Lens scoring \( k \) goals:
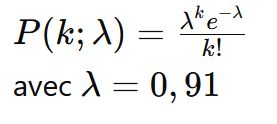
For Lens scoring k goals:
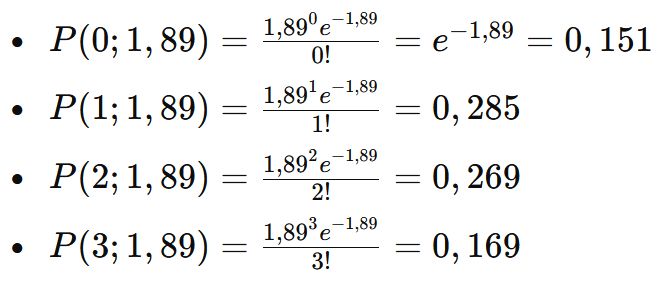
Calculating Score Probabilities for Lens
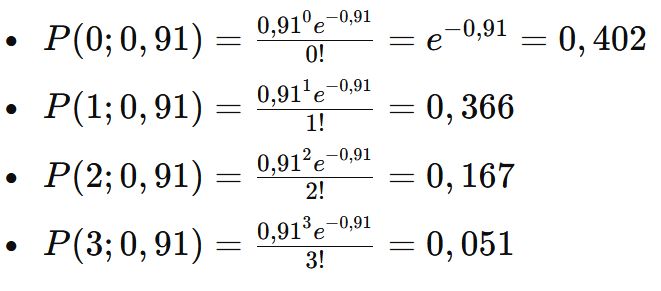
Step 4: Calculating Probable Scores
To obtain the combined probability of an exact score, we multiply the corresponding probabilities of each team. For example:
Probability of a 2-1 score in favor of Lille:
Step 5: Converting Probabilities to Odds
To convert these probabilities into odds, we use the following formula:
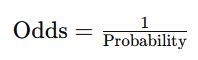
For a 2-1 score for Lille:
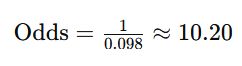
Limitations of the Poisson Distribution
Despite its usefulness, the Poisson distribution has certain limitations:
- It assumes events are independent, which is not always the case in football matches.
- It does not account for contextual factors such as injuries, weather conditions, or tactical changes.
- It is based on historical averages and may not reflect the current performance of the teams.
Conclusion
The Poisson distribution is a powerful tool for predicting exact scores in sports betting, providing a mathematical basis for estimating the probabilities of various outcomes. However, it is essential to recognize its limitations and use it in conjunction with other analyses to achieve more accurate and reliable predictions. By combining the Poisson distribution with a deep understanding of the teams and match circumstances, bettors can improve their strategies and increase their chances of success.
