In this article, we'll look at what makes a good punter, the fact that it's a skills competition, but also whether he's good enough to beat the bookmaker.

I've been wondering how many winners, or "sharps", there really are in sports betting. By "sharps" we mean someone who has a profitable expected return over the long term, not someone who is lucky.

Despite a large dose of uncertainty, I concluded that, for the most part, sharp bookmakers like Pinnacle probably ignore most of the square action from players they deem to be unskilled, at least in a relative sense. Of course, whether this is true will understandably remain a trade secret. It was thus comforting to see a prominent sports betting account on Twitter post the following.

“In most cases public money is ignored by most bookmakers. A very sharp old-time bookie once told me ‘I just stick public bets in my pocket like they don’t exist’”

It also became clear from such modis why. This is the topic of my latest article.

What makes a sharp bettor ?

Most sharps who make a living from their betting would likely agree on one piece of evidence as being indicative of the presence, or absence, of skill: can you make accurate lines, or odds, before the bookmakers do ?

Suppose I asked you to tell me the probability of Liverpool beating Manchester United, or the points total for the Los Angeles Lakers versus the Golden State Warriors; could you do it to within 1% of the bookmaker’s quotes ? It’s one thing seeing a price that’s already published and deciding whether it’s right or wrong. It’s quite another to predict the ‘correct’ number when you have no one else’s opinions to guide you.

Arguably, the majority of bettors will be heavily anchored to prior opinions about the probabilities of sporting outcomes. Indeed, this cognitive bias may provide one explanation for the

inefficiency of betting markets

.

Betting is a relative-skills competition

A common view of betting is that it represents a competition against the bookmaker. Beat the bookmaker and you will win. That’s true and it isn’t. Yes, there will be times when the bookmaker takes a position on some action. Beat them and they will lose money, whilst you will make a profit. But other times, they may not care what happens in a sporting event; they may profit either way.

In fact, the bookmaker is just one rather large player with a very unfair advantage (their betting margin). Really, a betting market should be viewed more like a financial market (of buyers and sellers), reflecting the opinions of many other players (backers and layers, or backers of different opinions) just like yourself, all expressing those opinions with their money.

The bookmaker simply reflects the flow of that money in their published odds for their most beneficial profit/liability trade-off, paying attention to some sources more than others.

If the published line or odds then reflects, to a greater or lesser extent, bettors’ opinions about the probability of Liverpool beating Manchester United or Los Angeles Lakers and Golden State Warriors scoring over 220 points, it is then clear that those who are the best at estimating the ‘true’ values stand the best chance of winning this competition. 

This competition is a relative-skills one. It is not simply enough to be good at estimating the ‘true’ numbers; you also have to be better than other people doing it. Novak Djokovic doesn’t win the Australian Open by being good at tennis, he wins it by being better than everyone else. Similarly, you’re not really getting paid for being right in a betting market; you’re actually getting paid for being more right than others.

Why the winner takes all ?

Unfortunately, the binary outcome of single bets (where you either win or you lose) hides this longer-term truth. When you get paid for winning one bet, it’s easy to be fooled by the illusion this game is just a matter of picking winners or beating the bookmaker.

But randomness dominates the small sample world of betting, with almost everything that happens happening because of chance. It is only over the longer term where the signal of this relative-skills competition begins to reveal itself.

This competition is iterative, where you play again and again, and small relative differences in predictive skills are compounded. Djokovic is only marginally more likely to win a single point than his opposition, but over the course of a 5-set match this translates into a much greater chance of overall victory. 

In the long run it is only the very best who will win. Betting then, like poker, is not just a relative-skills contest, it is also one where winners take all.

Sharp, then, does not mean absolutely sharp. It means relatively sharper than others, and relatively sharp enough to overcome the disadvantage imposed by the bookmaker, whose margin is really just representative of a very strong competitor.

Furthermore, getting absolutely sharper may not increase the chances of you winning, if everyone else is becoming absolutely sharper at the same time. Paradoxically, it may mean that your chances of winning through anything other than luck actually go down. Let’s look at a model to see how this plays out. 

Can you estimate an NBA games points total ? 

Most people don’t have an intuitive feel for probabilities. It’s much easier to answer the question who will win, Manchester United or Liverpool, than it is to ask: what are the probabilities of them winning? US sports, with leagues like the NBA, however, offer us the opportunity to work with numbers rather than percentages, since games consist of a large number of points. During the period 2007 to 2019 the average NBA game had about 200 points.

Let’s build a model where we ask competitors to estimate the number of points scored in an NBA game. We will set the model parameters as follows.

1. The ‘true’ number is 200.

2. On average the game will finish with 200 points, but randomness dictates there is a variance about this average figure. The standard deviation is set at 17.5, which is roughly the standard deviation in observed points totals for matches where the bookmaker sets the line at 200 points.

3. Eleven players will compete making the following match total estimates: 190, 192, 194, 196, 198, 200, 202, 204, 206, 208 and 210.

4. A random number generator determines the actual score of the game. Points are then awarded to players as follows:

a) Each player give to all the other players the points difference between their guess and the final total;

b) Each player receives from all other players the points difference between those players estimates and the final total. Obviously the better a player’s estimate the better their score relative to other players.

5. The competition is played over 10,000 matches. After each match the points totals of the 11 players are recalculated and the player with the most points is declared the winner.

6. A Monte Carlo simulation is used to determine the likelihood of each player being in the lead, i.e. a winner, after 100 matches, 1,000 matches and 10,000 matches.

The first chart below shows the probability of each player being the winning player after 100 matches, based on the Monte Carlo simulation output. Unsurprisingly, the player with the best estimate, 200 points, which matches the ‘true’ (average) total is winning most often. They have over a third chance of leading after 100 matches. Notice that even after 100 matches, the players with the weakest estimates are struggling to show any simulation victories, with the 6 weakest players accounting for less than 2.5% of the wins.

The next chart shows the probability of winning after 1,000 matches. Now only the best three players ever manage to register a victory, with nearly 86% going to the best player. As more rounds are played, the more the relative advantage the sharper players have is accumulated or compounded, and hence the more likely it is that they will win. On compound interest, for example, Albert Einstein is rumoured to have uttered: it is “the most powerful force in the universe.”

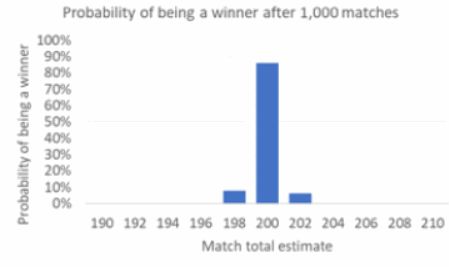
I haven’t bothered to show the chart after 10,000 matches. You can probably guess what it will look like. The 200-point player is winning every time.

The paradox of skill

What happens if we increase the absolute forecasting skills of the players? I re-ran the simulation, but this time with the following player estimates: 195, 196, 197, 198, 199, 200, 201, 202, 203, 204 and 205 match totals. 10 of the 11 players have become absolutely sharper. The next chart shows the percentage win distribution.

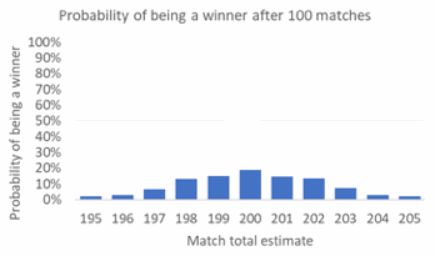
Despite the best player with an estimate figure the same as the ‘true’ number still being in the lead the most times after 100 matches, their chance of being so has fallen, from about 34% to about 19%. Similarly, the next best players are not doing as well, despite actually being absolutely sharper than they were in the first simulation.

The second-best player with an estimate of 198 points in the first simulation had a 22% probability of winning. Now, with an estimate of 199 points, that winning percentage has dropped to 15%. At the same time, the weakest players have a better chance of leading the competition. Now the six weakest players account for almost a quarter of the victories.

After 1,000 matches unsurprisingly the better players have an improved chance of winning, but still not as much as in the initial simulation.

What has happened between the first and second simulations? Firstly, it’s still ‘winner-takes-all’, it’s just this takes longer to play out. After 10,000 matches there were still 1.6% of winners who were not the best player.

Secondly, whilst players have become absolutely sharper in the second simulation, the variance between them has halved. Since the variance in outcomes is typically a combination of the variance in skill plus the variance in luck, if the former is reduced, the influence of the latter will increase. Paradoxically, as absolute sharpness across all competing players increases, and more importantly the range over levels in sharpness narrows, the influence that sharpness will have on their outcomes will fall. This is the paradox of skill.

If the vast majority of bettors are considered by bookmakers to be squares, doesn’t this make things much easier for those relatively sharp enough to become winners? Well, yes, you will beat the squares, but if the number of absolutely skilled players increases on the back of better modelling, it is likely that the variance across those skills will diminish. Better absolute skills then, but smaller relative differences.

Even if the bookmaker is ignoring most of the action of squares, their lines and prices will still reflect those players who are not, and the more markets you play in the more likely it is that you will be competing against them.

The next chart shows three relatively sharper players competing with eight relatively squarer players. None of the squares were winning after 1,000 matches in any of the 1,000 simulation runs.

Compare this distribution to the next one: more sharps, and on average absolutely sharper, but where the relative differences are smaller. Squares are still winning nothing, but the outcomes of the sharp players are now more defined by chance. Betting is a zero-sum, relative-skills competition where the winners take all, but the narrower the difference in skills across players, even subsets of players, the more that luck will define what happens to you. Now you know why some professional bettors have reported finding it harder and harder to stay a winner.

Are you good enough to beat the bookmaker ?

As I’ve already mentioned, the strongest competitor any bettor will face is the bookmaker, and that’s perhaps why so many still refer to the concept of beating them to make a profit. Not only do they have the best models (on average) but they can also reduce the effectiveness of yours by taking away some of your profit.

Just how good their models are can be seen in the final chart in this article. It compares their lines against actual match totals. The data comes from Sportsbook Reviews and consists of NBA closing line and scores for 15,508 NBA matches covering the period 30th October 2007 to 5th May 2019.

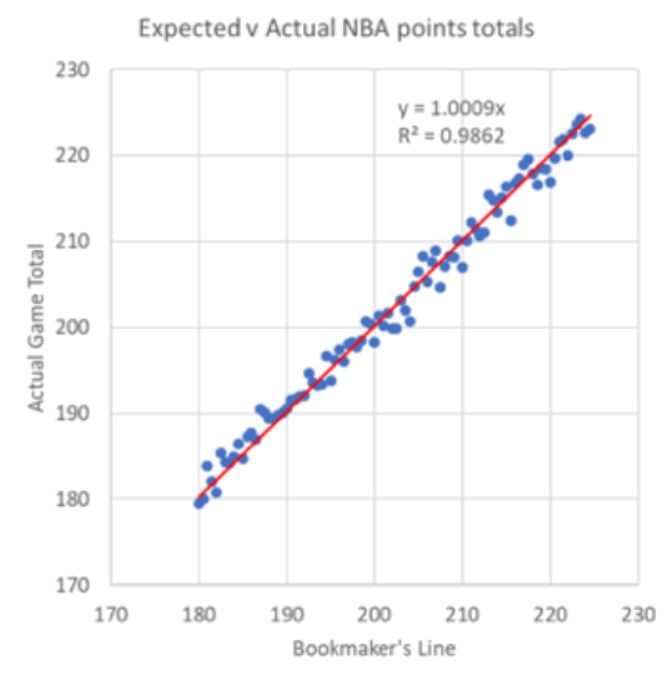
On average when the bookmakers quote a line of 190, 200 or 210, the match finishes with 190, 200 or 210 points respectively. Yes, there is a random variance in the results, and as already reported, it’s considerable. Nearly a third of games quoted with a 200-point line actually finish with fewer than 182 points or over 218 points.

But over the long term, the bookmakers are good - really good. To beat them, you have to overcome their margin. Prices of -105 or 1.95 (implying a 2.5% vig) mean you need to win about 51.3% of the time just to break even. With prices of -110 or 1.91 (and a 5% vig) this rises to 52.4%.

Given the standard deviation in observed results, that translates into about 0.5 and 1 point respectively. That might not sound like a lot, but can you find hundreds or thousands of matches where the bookmaker is relatively more wrong than you are by that much? Take a look again at the chart above and think about it.

What to remember if you’re serious about betting

Sports betting can be a lot of fun, and for most it should just be seen as a recreational hobby. But if you aspire to make any kind of living from it, or even just pay for your annual vacation, it is important to understand four things.

1. Betting is relative-skills competition. You don’t get paid for being good at predicting the future, you only get paid for being better at it than others.

2. Becoming sharper won’t necessarily turn you into a winner if others are getting sharper at the same time. The narrower the range of abilities, the more luck will dictate what happens to you.

3. Over the long run, the winners with relatively the best skills will take all. The competition is iterative, that is it is repeated many times, with even minor differences in skill over each iteration translating into very unequal reward distributions over time.

4. Finally, betting is a zero-sum game. The prize pool is finite and limited by the number of players. Losers pay for winners, and because of the winner-takes-all effect there are a lot more of the former than the latter.

Enjoy the ride, and never gamble what you can’t afford to lose.