Dans cet article, nous allons analyser un historique de paris réels, puis voir si battre la cote de clôture peut être due au hasard, avant de terminer par une comparaison de la ligne de clôture avec les profits/pertes.

En comparant les profits qu'un parieur a réellement réalisés avec ce qui aurait pu se passer par hasard, nous pouvons commencer à juger si l'historique est trop improbable pour être dû au hasard.

L'inconvénient de cette approche est le temps (ou plutôt le nombre de paris) qu'il peut falloir avant de pouvoir formuler des opinions plus concrètes.

Cote finale de Pinnacle

La cote finale de Pinnacle est la dernière cote disponible avant la fermeture d'un marché (juste avant le début d'un match) et est souvent utilisée comme mesure de succès pour les parieurs. Si les cotes que vous pariez sont plus élevées que la cote finale de Pinnacle, alors vous êtes considéré comme un parieur "avisé".

Un parieur misant typiquement sur des cotes autour de 5.0, par exemple, pourrait avoir besoin de 2 500 paris avant de pouvoir être sûr qu'une telle performance n'était probablement pas seulement due à la chance - s'il faisait cinq paris par jour, cela prendrait plus d'un an. Malheureusement, l'étendue des possibilités dues au hasard est vaste, et il faut beaucoup de temps pour que la loi des grands nombres exerce son influence.

Heureusement, il existe une approche alternative, que j'ai évoquée précédemment en examinant ce que la ligne de clôture peut nous dire sur les attentes de profit. Il y a des preuves convaincantes que la marge par laquelle vous dépassez la ligne de clôture (ou les cotes) est un prédicteur fiable de votre rentabilité.

Si vous dépassez la ligne de clôture de 10 %, vous devriez vous attendre à réaliser un profit sur le chiffre d'affaires de 10 % à long terme, ce qui implique que la ligne de clôture reflète avec précision les chances "réelles" des résultats sportifs. De telles cotes sont dites efficientes.

Certainement, il y a des parieurs profitables qui échouent à dépasser la ligne de clôture et qui contestent donc cette hypothèse. Pour ces derniers, deux possibilités doivent exister : soit ils ont tort et sont chanceux et finiront par régresser vers la moyenne. Soit, l'hypothèse de la ligne de clôture efficiente n'est pas tout à fait correcte, et il existe des lignes, systématiquement identifiées par ces parieurs, qui n'ont pas atteint les prix "réels".

Dans cet article, je n'ai pas l'intention d'aborder la faiblesse potentielle de cette hypothèse, il suffit de dire que j'ai déjà discuté d'une manière possible dont les cotes de clôture pourraient systématiquement (c'est-à-dire non aléatoirement) dévier de l'efficacité totale. Cela pourra être abordé une autre fois.

Au lieu de cela, dans cet article, je veux examiner comment nous pourrions théoriquement utiliser la ligne de clôture pour tester les compétences du parieur, étant donné que l'hypothèse de la ligne de clôture efficiente est vraie. Après tout, Marco Blume, ex-Directeur du trading chez Pinnacle, a déclaré que la ligne de clôture est en moyenne très, très précise, que les parieurs avisés la battent, et que ses traders essaient d'atteindre la ligne la plus efficiente avec les informations dont ils disposent. Pour les besoins de ce qui suit, prenons-le au mot.

Analyse d'un historique de paris réel

Le graphique suivant montre l'historique des profits à mises fixes d'un parieur réel, composé de 1 214 paris sur une période de 11 semaines au début de 2019, avec des cotes moyennes de 2.065 et un profit sur chiffre d'affaires de 5,73 %.

La ligne bleue montre la performance réelle, la ligne rouge la performance attendue. De toute évidence, l'historique réel a surperformé par rapport aux attentes. Comment ai-je calculé le profit attendu ?

Dans leur historique de paris, le parieur a soigneusement enregistré toutes les cotes qu'il a placées et toutes les cotes de clôture pour ces paris. Comme mentionné précédemment, le ratio de ces deux cotes nous offre une estimation fiable de l'avantage attendu par les parieurs. Bien sûr, les deux cotes contiennent la marge du bookmaker. Nous devons la retirer de la cote de clôture pour calculer une estimation du prix "juste" ou "réel", en supposant une efficacité totale des prix à la fermeture du marché.

En retirant la marge, j'ai également pris en compte le biais favori-longshot, qui voit les outsiders attirer une plus grande part de la marge du bookmaker que les favoris.

Le premier pari de la série, par exemple, a été placé à 2.13. Il a fermé à 1.85. Après avoir retiré la marge du bookmaker, le "vrai" prix de clôture était de 1.89. Par conséquent, l'avantage attendu que le parieur détenait était de 2.13/1.89 = 12.8%. Cela signifie que pour chaque 100 paris de 1 unité placés de cette manière, un profit de 12.8 unités pourrait être attendu.

L'avantage moyen détenu était de 2.19 %, ce qui implique un profit attendu sur chiffre d'affaires de 2.19 %. Le prix moyen de clôture "juste" était de 2.024.

Le dépassement de la ligne de clôture peut-il se produire par hasard ?

Pour enquêter sur la manière et la raison pour lesquelles un parieur peut dépasser le prix de clôture de cette manière, nous devrions commencer par estimer la probabilité que cela se produise par hasard. Pour ce faire, j'ai à nouveau puisé dans une population de 162 672 cotes d'ouverture et de clôture de paris sur des matchs de football de Pinnacle que j'avais analysée dans un de mes articles précédents.

Dans cet échantillon, 35,7 % des cotes d'ouverture des paris domicile et extérieur (avec des valeurs moyenne et médiane de 3.443 et 2.75 respectivement) détenaient théoriquement un avantage rentable sur leurs "vraies" cotes de clôture. Le ratio moyen des cotes d'ouverture aux cotes de clôture "justes" pour cet échantillon était de 0.969 %, ce qui implique une perte attendue sur mises fixes de -3.1 %.

Si nous choisissions au hasard 1214 paris de cet échantillon, nous devrions nous attendre à ce que le ratio moyen soit de 0.969. Bien sûr, nous n'obtiendrions pas toujours 0.969, tout comme nous n'obtenons pas toujours 10 piles et 10 faces lorsque nous lançons une pièce 20 fois. Quelle serait la probabilité de choisir au hasard un échantillon montrant un ratio moyen de 1.000, impliquant une attente d'équilibre ?

Nous pouvons répondre à cette question si nous connaissons l'écart type des ratios de cotes d'ouverture et de cotes "justes" de clôture. Dans cet échantillon, il était de 0.114 (ou 11.4 %), ce qui signifie qu'environ les deux tiers des ratios de cotes individuels se situaient entre 0.855 et 1.083, comme défini par la distribution normale.

Avec cette information, nous pouvons estimer quel serait l'écart type dans le ratio moyen des cotes d'un échantillon de 1 214. C'est-à-dire, si nous avions un grand nombre d'échantillons de 1 214 paris avec des cotes comme celles de ma population ici, nous voulons connaître l'écart type dans le ratio moyen des cotes à travers ces échantillons.

Les lecteurs de mon article sur la modélisation de vos possibles retours de paris peuvent se rappeler que l'écart type dans la moyenne d'une métrique de pari, comme le rendement ou dans ce cas le ratio des cotes d'ouverture à de clôture, est inversement proportionnel à la racine carrée du nombre de paris. Ainsi, l'écart type du ratio moyen des cotes ici peut être calculé en divisant 0.114 par la racine carrée de 1 214. La réponse est 0.0033.

En d'autres termes, pour des échantillons de 1 214 paris avec des cotes comme ma population ici, environ les deux tiers se situeront entre 0.966 et 0.972. Avec cette valeur, nous pouvons maintenant calculer la probabilité qu'un ratio moyen des cotes d'ouverture aux cotes "justes" de 1.000 dans un échantillon de 1 214 paris se produise par hasard, compte tenu d'une valeur attendue de 0.969. La réponse est effectivement de 0 % (en fait environ 1 sur 100 millions de trillions pour être plus précis). Étant donné que 1.000 est à plus de neuf écarts types de 0.969, ce résultat ne surprendra personne familiarisé avec les statistiques de la distribution normale.

Preuve d'un parieur compétent

L'implication de cette analyse est claire. Si un parieur devait montrer un ratio moyen des cotes de pari aux cotes de clôture "justes" de 1.000

 alors que l'attente est de 0.969 dans un échantillon de 1 214 paris, cela ne peut catégoriquement pas être dû à la chance. Au lieu de cela, l'explication doit être causale ; la plus évidente étant la compétence du parieur et la réaction du bookmaker en raccourcissant leurs cotes. Si ce n'est pas l'explication, nous avons toujours besoin d'une autre explication causale ; pour réitérer, cela ne peut pas être de la chance.

Revenons à notre parieur réel et à son historique. Tout d'abord, nous devrions reconnaître que ses cotes moyennes, 2.065, sont significativement différentes des cotes moyennes dans ma population d'analyse, 3.443. Comment cela change-t-il les calculs ?

Plus les cotes sont élevées, plus elles sont susceptibles de bouger. Encore une fois, ce n'est pas une observation surprenante. Si nous déplaçons une proposition de 80%/20% de 5% à 75%/25%, le favori passera de 1.25 à 1.333 (un ratio de 0.9375) tandis que l'outsider passera de 5.0 à 4.0 (un ratio de 1.25). En fait, l'écart type dans le ratio des cotes d'ouverture à de clôture est proportionnel au logarithme des cotes. Les cotes de 1.25 voyaient typiquement un écart type d'environ 0.043, tandis que les cotes de 5.0 avaient une valeur d'environ 0.14.

De même, le ratio moyen des cotes d'ouverture aux cotes de clôture "justes" change avec les cotes moyennes, diminuant à peu près linéairement à mesure que les cotes augmentent. Les cotes de 1.25 montrent un ratio moyen d'environ 0.99, tandis que les cotes de 5.0 montrent un chiffre d'environ 0.95.

Les cotes moyennes du parieur de 2.06 auraient un écart type d'environ 0.079 et autour d'une moyenne de 0.98. Diviser cet écart type par la racine carrée de 1 214 nous donne une valeur de 0.0022, donc à nouveau un ratio de 1.000 est à environ neuf écarts types de l'attente de 0.98.

Enfin, nous devrions nous rappeler que le parieur ici n'a pas seulement égalé le prix de clôture "juste" en moyenne. Ils l'ont battu de 2.19 %. Les chances de faire cela alors que l'attente est de -2.0 % ? Environ une sur un quattuorvigintillion (1 avec 75 zéros) ou environ 18,5 écarts types. Ce parieur faisait bouger les lignes, et c'est parce que le bookmaker les reconnaissait comme quelqu'un avec de meilleures connaissances que le reste du marché au moment où ils ont parié les cotes publiées.

Il est utile de rappeler brièvement aux lecteurs que j'ai également tenté de modéliser la fréquence à laquelle un parieur devrait théoriquement dépasser le prix de clôture "juste" pour avoir une valeur attendue profitable. Le chiffre auquel je suis arrivé était d'environ 70 %. Notre parieur a dépassé le prix de clôture "juste" 73,5 % du temps (dépassant le prix de clôture publié 84,2 % du temps).

Valeur de la ligne de clôture versus profits et pertes

Revenons à l'historique des profits/pertes (P/L) du parieur. En utilisant mon approche traditionnelle de test de signification, une telle performance pourrait éventuellement se produire par hasard environ une fois sur 200 parieurs. Sur cette base, il est probable que quelque chose de plus que de la chance soit en jeu, mais si nous avions un échantillon de 200 parieurs et que c'était le meilleur historique, nous ne pourrions pas vraiment exclure la possibilité qu'il n'y ait aucune compétence.

Comparez cela à la méthodologie de la valeur de la ligne de clôture (CLV) que j'ai décrite ci-dessus. Un sur 200 contre un sur un quattuorvigintillion. Laquelle nous donne des informations plus fiables sur la probabilité de la compétence du parieur ?

Le graphique ci-dessous compare les deux approches pour un parieur pariant des cotes de 2.00, illustrant à quelle vitesse la méthodologie CLV fournit des informations significatives au parieur sur ses chances d'être un gagnant à long terme avec un avantage attendu de 2 %. L'axe y est logarithmique, mesurant les chances qu'un profit attendu/réel sur chiffre d'affaires de 2 % se produise par hasard pour les méthodes CLV et P/L respectivement.

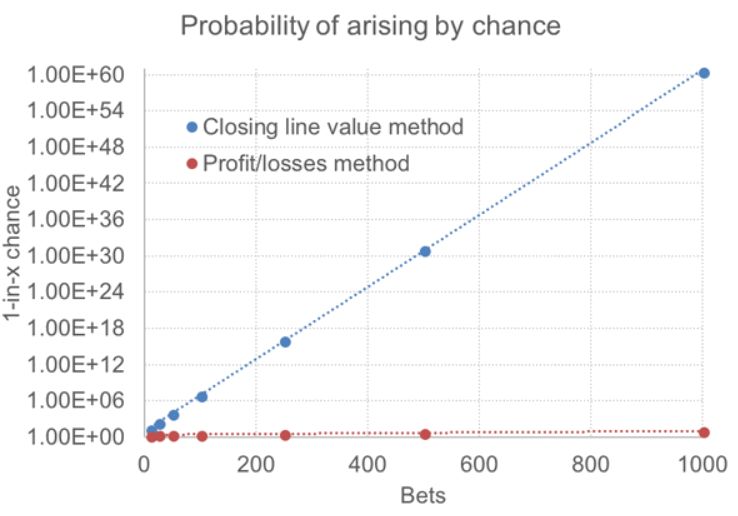
Comparé à la méthode CLV, en utilisant les profits et pertes réels ne s'inscrit même pas. Même après 1 000 paris, il n'y a qu'une probabilité de 1 sur 10 que la chance ait pu offrir un profit de 2 % alors que l'attente est une perte de 2 %. Les statisticiens testant des hypothèses ne cligneraient même pas des yeux. Si un tel parieur devait montrer un rendement attendu de 2 % basé sur la manière dont ils dépassent les prix de clôture justes des paris qu'ils font, seulement 50 d'entre eux fourniraient la confiance de savoir que cela se produirait une fois sur environ 10 000 fois.

Bien sûr, vous pourriez à juste titre souligner que les profits et pertes sont réels et que les lignes de clôture nous donnent juste une idée de ce à quoi s'attendre. À cette mesure, notre parieur a très bien réussi avec un rendement proche de 6 %. Le point clé ici, cependant, est qu'il faut beaucoup plus de temps pour séparer le hasard de la causalité avec les profits et pertes qu'avec la valeur de la ligne de clôture.

À condition que l'hypothèse de la valeur de la ligne de clôture soit correcte (elle ne l'est peut-être pas complètement, mais cela sera abordé une autre fois), elle fournit un indicateur beaucoup plus fiable de la compétence du parieur qu'un simple historique de paris. On pourrait dire que dépasser la ligne de clôture "juste" nous en dit beaucoup plus sur l'attente à long terme de ce parieur. Possiblement les deux tiers de la rentabilité réelle de notre parieur sur 1 214 paris présentés dans cet article étaient dus à la chance. À long terme, ils peuvent s'attendre à régresser vers 2.19 %.

Conclusion

Je sais qu'il y aura encore des parieurs avec des historiques rentables qui échouent à dépasser la ligne de clôture et qui diront : "Mon historique ne prouve-t-il pas simplement que l'hypothèse de la valeur de la ligne de clôture efficiente est invalide pour estimer la rentabilité attendue ?" Oui, peut-être, mais il y a deux points qui doivent être pris en considération.

Premièrement, si un parieur dépasse la ligne de clôture de la manière dont notre parieur l'a fait dans cet article, nous devons l'expliquer. La chance seule ne peut pas le faire comme les chiffres l'ont prouvé. La réponse évidente est qu'ils sont compétents et que le bookmaker le sait.

Par conséquent, si un parieur rentable peut déplacer les lignes, pourquoi pas un autre ? À moins qu'un tel parieur ne puisse offrir des explications raisonnables et testables pour expliquer pourquoi ils ne le font pas, il doit rester probable qu'ils ont simplement eu de la chance. Rappelez-vous, vous pourriez avoir un historique de paris de 1 sur un million, mais si vous êtes le meilleur parmi un million de parieurs traçables, que signifie vraiment cela ?

Deuxièmement, avec ces informations, la ligne de clôture agit comme une jauge, permettant au parieur de mesurer très rapidement sa performance attendue. Étant donné que même de petites déviations par rapport aux attentes sont très improbables sur des échantillons aussi petits que 50 paris, le parieur pourra identifier très rapidement si le marché pense qu'ils ont perdu leur avantage. C'est quelque chose de totalement impossible avec l'analyse des profits/pertes seule. Dans les mots de notre parieur ici, "Je peux utiliser la CLV comme un détecteur de falaise, de cette façon je peux ralentir, ou changer ma direction, pour ne pas tomber."

Jusqu'à ce que les bookmakers nous montrent les données sur les profits/pertes par rapport à la valeur de la ligne de clôture, nous ne saurons jamais à quel point un indicateur CLV est vraiment fiable. Une grande partie de mon analyse de données publiée dans les ressources de paris de Pinnacle au fil des ans suggère que, si ce n'est pas parfait, c'est sûrement assez bon.

Après tout, Marco Blume nous a dit que les parieurs avisés déplacent les lignes. Qui suis-je pour argumenter avec cela ? Donc, si vous avez la présence d'esprit de garder un historique de vos cotes de paris, gardez également les prix de clôture, et vous pouvez déterminer très rapidement si votre bookmaker et le marché pensent que vous êtes un gagnant.