Dans cet article, vous allez apprendre la réinterprétation des différents plans de mise avec la formule de Kelly, mais aussi les explications de l'impact sur la perte et/ou le gain d'unités, l'asymétrie des rendements, et la symétrie de la probabilité.

Il y a 4 ans, un article a été publié dans le journal "Économie du Sport", sur la manière dont un parieur rentable devrait miser dans des conditions où les estimations des véritables probabilités de gain ne sont pas disponibles.

La question de savoir si un parieur souhaitant avoir une rentabilité constante sur le long terme devrait même être actif dans de telles conditions est discutable, mais il s'avère que de nombreux parieurs sportifs reconnaissent qu'ils ne sont pas en mesure de les estimer avec précision.

Néanmoins, leur étude est intéressante dans la mesure où elle montre comment différents plans de mise peuvent être réinterprétés comme des variantes du critère de Kelly. Dans cet article, je souhaite résumer leurs efforts et examiner si ce qu'ils ont découvert peut être amélioré.

Réinterpréter les différents plans de mise avec la formule de Kelly

Il n'y a peut-être pas de sujet plus populaire dans le monde de la gestion de l'argent des paris sportifs que l'utilisation du critère de Kelly comme méthode de mise. J'ai notamment démontré que pour une mise Kelly simple, où une seule mise à la fois est placée avant le règlement, la stratégie est capable de prendre en compte les risques liés au fait de ne pas connaître précisément votre avantage sur la base d'une mise à la fois, tant que vous êtes précis en moyenne.

Perte unitaire

La première de ces stratégies est la perte unitaire, ou méthode des enjeux nivelés, selon laquelle le parieur risque la même mise sur chaque pari, quelle que soit la cote. Plus la cote est élevée, plus l'impact sur la bankroll est important dans le cas où le pari est gagnant, mais plus la probabilité que le pari soit gagnant est faible.

Nous pouvons considérer la mise sur les pertes unitaires comme un plan Kelly dans lequel la valeur attendue ou le rendement est linéairement proportionnel à la cote. Étant donné que la taille de la mise Kelly est donnée par EV / cote - 1 (où EV est la valeur attendue, tout ce qui est supérieur à 0 étant considéré comme rentable), un plan de perte unitaire implique que ce ratio reste constant.

Par exemple, supposons que l'EV (Valeur Attendue) soit de 10% (0,1) et la cote de 2,00. La mise serait de 0,1. Si la cote passe à 4,00, cela signifie que l' EV doit passer à 30 % (0,3) pour que l'enjeu reste à 0,1. Une cote de 101,00 impliquerait une EV de 10 ou 1 000 %, ce qui semble un peu irréaliste. Cela impliquerait une cote réelle de seulement 9,18. Il est certain qu'aucun bookmaker ne commettra une erreur aussi grave.

En effet, dans la limite où les cotes tendent vers l'infini, les cotes réelles tendraient vers une valeur maximale donnée par 1 / enjeu, dans ce cas 10. L'une des principales critiques formulées à l'encontre du staking sur les pertes unitaires est qu'il fait peser un risque trop important sur les paris à long terme dont les probabilités de gain sont faibles. Pour les défenseurs du critère de Kelly, cela n'aurait du sens que si l'EV augmentait réellement de manière proportionnelle à la cote, ce qui, comme nous pouvons le voir, est difficilement crédible.

Gain unitaire

Le deuxième plan de gestion de l'argent généralement utilisé par les parieurs est le pari à l'unité. Dans ce cas, la mise est telle que le parieur vise à réaliser le même profit quelle que soit la cote. Si l'objectif de gain, ou de profit, est de 100 €, une cote de 2,00 nécessitera une mise de 100 €, tandis qu'une cote de 5,00 nécessitera une mise de 25 €. La taille de la mise est proportionnelle à la réciproque de la cote - 1. En termes de Kelly, la stratégie de gain unitaire implique que l'EV n'est absolument pas corrélée avec le critère de Kelly ; toutes les EV sont les mêmes quelles que soient les cotes.

En ce qui concerne les paris sur les pertes unitaires, il y a quelque chose qui ne va pas. Est-il possible que l'avantage d'un parieur soit le même, que la cote soit de 1,11 ou de 111,00 ? Les leçons tirées de la variance suggèrent que cela n'est pas très réaliste. En effet, si votre EV pour une cote de 111,00 est de 20 % (0,2), la même VE pour une cote de 1,11 impliquerait que la véritable cote est inférieure à 1, ce qui est tout à fait absurde. Quelque chose ne peut pas avoir une probabilité de résultat supérieure à 100 %.

Impact de l'unité

Les auteurs ont proposé un plan de mise alternatif : l'impact unitaire, en faisant l'hypothèse que ce plan s'accorde mieux avec la méthode de mise de Kelly. La méthode de l'impact unitaire maintient constante la différence de bankroll entre gagner et perdre, et ce, quelle que soit la longueur ou la brièveté des cotes.

L'enjeu de l'impact unitaire est proportionnel à la réciproque de la cote, contrairement au gain unitaire qui est la réciproque de la cote - 1. Ainsi, si la mise est de 100 € pour une cote de 2,00, la mise d'impact unitaire pour une cote de 5,00 sera de 40 €. Dans chaque cas, la différence entre le gain et la perte est de 200 € (+100 €/100 € dans le premier cas et +160 €/40 € dans le second).

Pour les paris à impact unitaire, l'EV est proportionnelle à la cote - 1 / cote. Cela signifie que l'EV augmente avec l'augmentation des cotes, mais à un taux décroissant vers une limite, puisque ce ratio tend rapidement vers 1. Par exemple, si l'EV = 0,1 pour une cote de 2,00, la limite de l'EV sera de 0,2. Bien que ce scénario ne soit pas aussi extrême que pour le pari sur les gains unitaires, où l'EV reste inchangée, il semble à nouveau sous-estimer la possibilité d'EV plus élevées pour des cotes plus longues.

Les pronostiqueurs de courses de chevaux qui réussissent ont généralement des rendements nettement supérieurs au double de ceux qui se concentrent sur le marché des handicaps asiatiques ou des écarts de points, bien que cela ne signifie pas nécessairement qu'ils sont plus compétents (ou plus chanceux) ; ils ont simplement une plus grande variance de leur côté.

En suivant les indications de l'auteur, le tableau ci-dessous illustre comment l'EV varie en fonction des cotes pour les trois différents plans de mise, en supposant que l'EV = 3 % pour des cotes = 2,00 pour chacun d'entre eux.

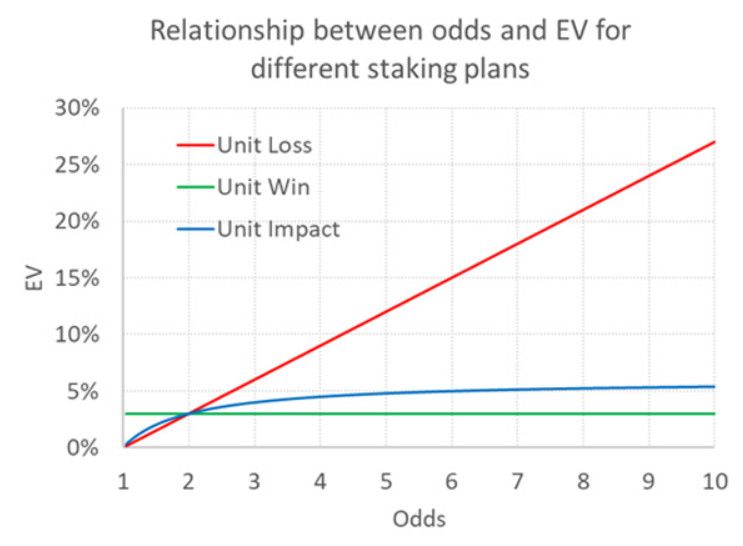
Comme nous l'avons vu précédemment, les plans de mise "perte unitaire" et "gain unitaire" semblent tous deux impliquer des relations irréalistes entre les cotes et l'EV.

Les auteurs ont analysé la base de données de choix de paris d'un site de pronostics bien connu et pensent avoir confirmé que la relation entre la VE et la cote impliquée par la mise sur l'impact unitaire reflète le mieux les rendements observés et attendus des pronostiqueurs (ces derniers étant basés sur les prix de clôture). Je ne suis toujours pas convaincu. Je le répète, la méthode de l'impact unitaire ne produira jamais qu'une EV qui est au maximum le double de l'EV pour des cotes = 2,00. Existe-t-il une meilleure alternative ?

Réexamen de la distribution T

Il y a trois ans, j'ai présenté l'utilisation de la distribution T pour évaluer les pronostiqueurs et distinguer la chance de l'habileté. Similaire à la distribution normale (et utilisée à sa place lorsque l'on ne connaît que l'écart type de l'échantillon et non celui de la population), elle permet de déterminer le degré d'improbabilité d'un échantillon donné en supposant que la moyenne de la population est connue.

J'ai beaucoup utilisé la distribution T dans mon travail pour aider les parieurs à déterminer la probabilité que leurs résultats soient le fruit du hasard, en supposant qu'ils n'aient aucune compétence. Plus la probabilité est faible, plus vous pouvez être subjectivement confiant dans le fait que le hasard n'a rien à voir avec les bénéfices de vos paris.

Au cœur de ce test se trouve la statistique t ou le score t, à partir duquel les probabilités peuvent être dérivées. J'ai montré que pour un pari à perte unitaire, et lorsque les cotes de votre record ne varient pas trop, cette statistique peut être approximée avec la formule suivante.

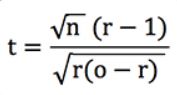
où n est le nombre de paris, o la cote moyenne et r le retour sur investissement ou le rendement + 1.

Comme le z-score, que les handicapeurs connaissent peut-être mieux, il s'agit essentiellement d'une mesure du nombre d'écarts types que votre rendement s'écarte d'une moyenne attendue de zéro, si vous pariez sans compétence et à des cotes équitables. Un score t de 2, par exemple, signifie qu'un meilleur rendement que celui obtenu par votre record n'est attendu que 2,5 % du temps, en supposant que vous n'ayez aucune compétence. Le score t est donc un type de mesure de la probabilité. Plus le score t est élevé, moins l'observation est probable. Utilisons-le pour déterminer la probabilité de différentes EV (en supposant qu'il n'y ait aucune compétence) en fonction des cotes que nous misons.

L'asymétrie des rendements

Supposons que vous pariez sur une équipe ayant 80 % de chances de gagner, avec une cote de 1,25. Supposons maintenant que le bookmaker pense à tort que la probabilité de victoire est de 75 %. Il fait une promotion et n'a pas de marge. Sa cote est de 1,333. Par conséquent, votre VE est de 6,667 % (1,333/1,25 - 1 ou 0,80/0,75 - 1).

Considérons maintenant un deuxième scénario : la véritable chance est de 20 % (cote équitable de 5,00), mais le bookmaker estime qu'elle est de 15 % (cote publiée de 6,667). Cette fois, votre EV est de 33,33 % (6,667/5,00 - 1 ou 0,20/0,15 - 1). La différence de pourcentage de gain attendu entre votre estimation et celle du bookmaker est la même, mais l'EV est 5 fois plus importante. Il semble qu'en termes d'EV, les erreurs équivalentes soient d'autant plus sanctionnées que les cotes sont élevées. Mais quelle est la probabilité de ces erreurs ?

La symétrie de la probabilité

Réécrivons la formule du score t ci-dessus (en supposant que tous nos paris ont la même cote, o). Puisque nous savons que r = q / p, où p est la probabilité implicite de la cote du bookmaker (c'est-à-dire 1/o) et q est votre probabilité estimée (qui est "vraie" si votre modèle de prévision est précis), on peut démontrer que :

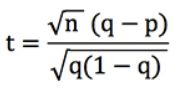
Supposons que n, notre nombre de paris, soit égal à 100. Pour q = 0,8 et p = 0,75, t = 1,25. De même, pour q = 0,2 et p = 0,15, t = 1,25 également. En supposant que le bookmaker, et non notre modèle, soit réellement correct, un tel score t correspondrait à une probabilité de résultat de 10,7 % (en utilisant la fonction =TDIST d'Excel).

Sur 100 paris, nous devrions obtenir un rendement supérieur à 6,667 % pour une cote de 1,333, ou supérieur à 33,33 % pour une cote de 6,667, soit 10,7 % du temps. Des rendements plus importants à des cotes plus élevées sont tout aussi probables que des rendements plus faibles à des cotes plus courtes ; c'est pourquoi les pronostiqueurs de courses ont l'illusion d'être meilleurs que les handicapeurs, ou bien pires s'ils sont perdants.

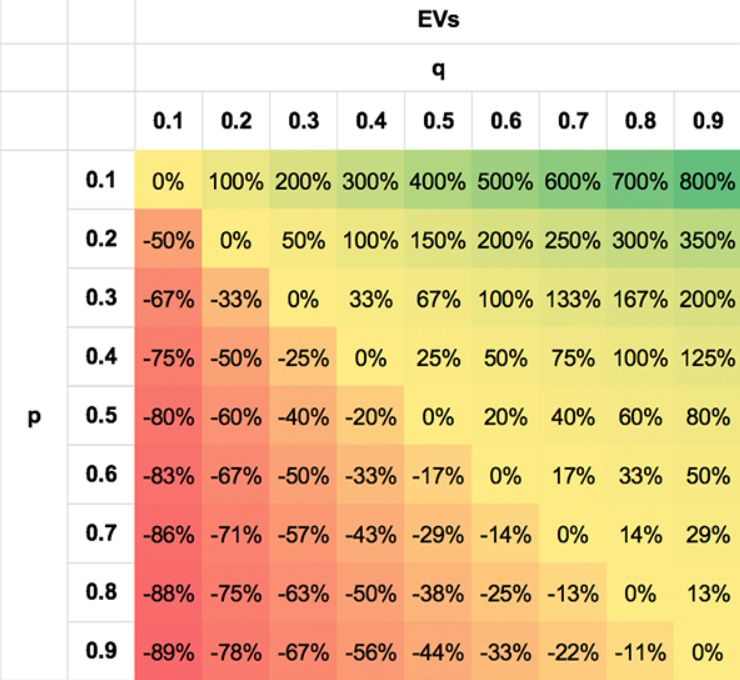
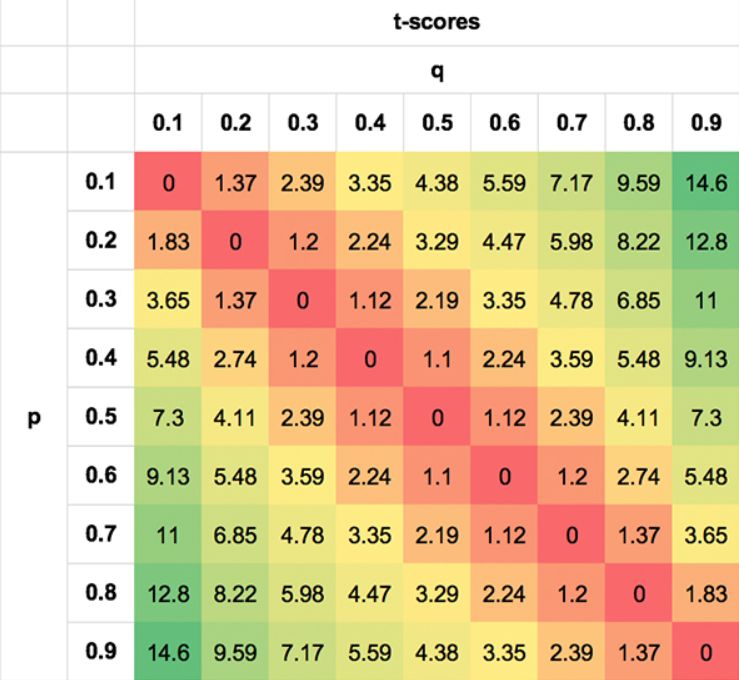
J'ai tenté d'illustrer cette symétrie des probabilités à l'aide des tableaux suivants. Les valeurs sont extrêmes simplement pour illustrer le propos ; il est évident qu'aucun parieur ne sera en mesure de faire cela bien, ou mal, pour la plupart des scénarios.

La première montre l'asymétrie de l'EV pour différentes paires p, q. La seconde montre la symétrie des t-scores. Le second montre la symétrie des t-scores. J'ai indiqué les t-scores absolus (en supprimant le signe négatif pour les EV négatives lorsque q < p) pour plus de clarté. Non seulement une paire p, q de 0,3/0,7 est tout aussi probable qu'une paire 0,7/0,3, mais il en va de même pour des paires telles que 0,7/0,5 et 0,3/0,1, 0,8/0,7 et 0,2/0,1 pour les raisons décrites ci-dessus.

Une nouvelle fonction de cote EV-

Pour une cote et une EV données, il existe une probabilité t (qui double lorsque le nombre de paris est multiplié par 4). Nous pouvons réarranger la formule du score t pour l'exprimer en termes de r. Cela conduit à une quadratique plutôt horrible avec une solution encore plus horrible.

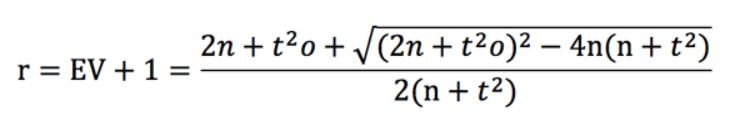
C'est une solution bien plus désagréable que cote - 1 / cote, mais représentons-la quand même pour le scénario où EV = 0,03 et cote = 2,00. Ce graphique est présenté ci-dessous, ainsi que les fonctions EV précédentes pour la perte unitaire, le gain unitaire et l'impact unitaire de la mise.

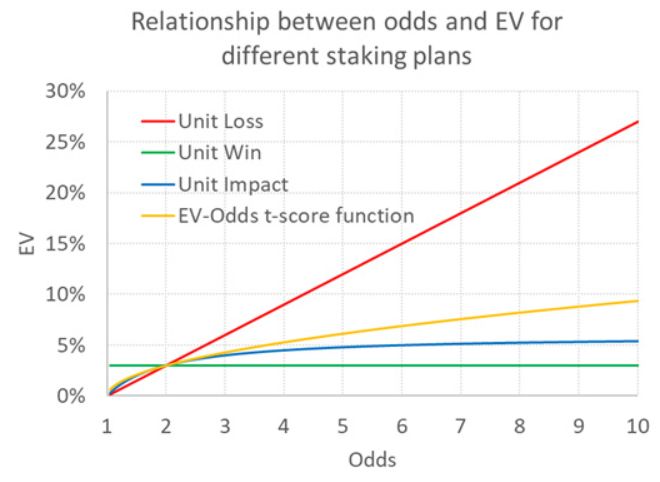
Bien que la fonction puisse être difficile à écrire, elle est plus intuitive car elle interprète les rendements attendus en termes de probabilité statistique. Pour les paris à impact unitaire, l'EV ne peut jamais être supérieur à 6 % lorsqu'il est de 3 % pour des cotes de 2,00. Mais avec ma fonction, elle peut croître indéfiniment, même si ce n'est pas à une vitesse aussi irréaliste que pour les paris sur les pertes unitaires, mais conformément à ce que prédit la variance statistique. Pour des cotes de 10, il est de 9,4 %, pour des cotes de 50, il est de 23,3 % et pour des cotes de 1 000, il est de 150 %.

Une critique évidente est que cette fonction, basée sur le score T, suppose que le parieur n'a aucune compétence. Elle exprime simplement la probabilité que les choses se produisent en supposant qu'aucune compétence n'est présente. Mais il s'agit d'une interprétation erronée ; même en présence de compétences, les mêmes lois statistiques associées à la variance s'appliquent.

La position de la courbe orange changerait, mais la forme resterait la même. J'ai illustré ci-dessous quelques trajectoires possibles pour des parieurs ayant divers degrés de chance ou d'habileté, selon le terme utilisé. La courbe initiale du parieur ayant une VE de 3 % pour une cote de 2,00 est toujours représentée en orange.

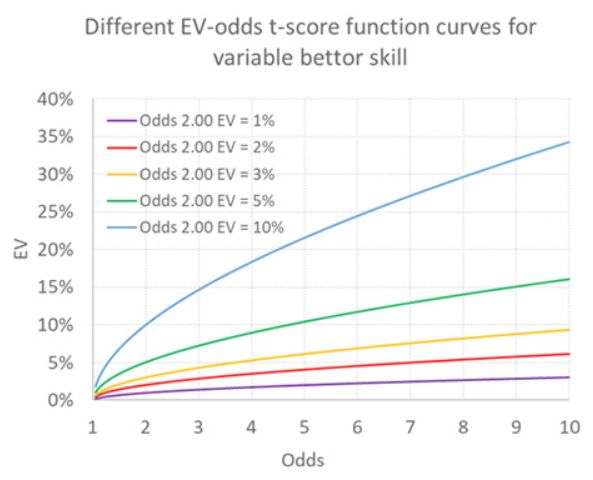
Une autre critique pourrait être que nous supposons également que toute compétence est indépendante des cotes, c'est-à-dire qu'elle est la même quelles que soient les cotes. Compte tenu des inefficacités du marché, telles que le biais favori-long terme, cette hypothèse n'est peut-être pas appropriée.

Test de la fonction

Pouvons-nous tester la validité de cette nouvelle fonction EV ? Mon système de paris "Wisdom of the Crowd", que ceux qui me suivent régulièrement sur Twitter et Football-Data connaissent bien, utilise les cotes plus efficaces de Pinnacle pour estimer l'EV disponible dans les cotes des autres bookmakers.

À partir d'un échantillon de données de cotes de matchs des championnats nationaux européens remontant à la saison 2012/13, j'ai trouvé 55 237 occasions où une EV rentable (>0) était disponible. La moyenne était de 2,20 % (pour mémoire, la performance réelle des enjeux de perte unitaire était de 1,77 %, bien en deçà des marges statistiques d'erreur du modèle), avec des cotes moyennes de 3,30. Avec ces chiffres, nous pouvons utiliser ma formule de solution quadratique pour construire une courbe de fonction EV- comme celles ci-dessus. Il s'agit de la courbe orange ci-dessous.

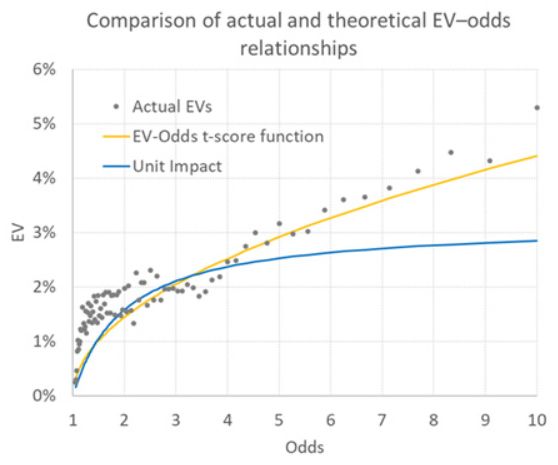
Comparez cette courbe, d'une part, aux EV du modèle réel calculées en fonction des espérances de gain de 1 % (indiquées sous forme de cotes dans le graphique) et, d'autre part, à la courbe de la fonction EV prédite par la mise à l'impact unitaire. Bien que la correspondance ne soit pas parfaite, la fonction EV t-score permet sans doute de mieux prédire les EV approximatives basées sur les cotes des paris.

Un raisonnement

Les plus observateurs d'entre vous pourraient maintenant se dire : quel est l'intérêt d'utiliser une fonction EV pour prédire l'EV pour différentes cotes alors que votre modèle de sagesse de la foule le fait explicitement pour chaque pari ? Il s'agit en effet d'un jugement valable, et une grande partie de cet article pourrait donc être considérée comme plutôt théorique.

Néanmoins, même les modèles précis (en moyenne) présentent une incertitude épistémique pour chaque pari. En outre, l'incertitude aléatoire (ou inhérente) rend l'évaluation des véritables probabilités de gain pratiquement impossible.

L'objectif de cet exercice, comme pour les auteurs, était donc d'illustrer la manière dont on peut tenter d'estimer approximativement sa EV lorsque l'on reconnaît ces incertitudes quantitatives, lorsque le modèle de prédiction n'estime pas explicitement les probabilités de victoire, ou lorsque la méthode de prévision est plus qualitative et repose sur des intuitions plutôt que sur l'analyse de données. Si vous connaissez vos probabilités, cette méthode vous permettra d'estimer votre EV ; si vous connaissez votre EV, vous pourrez alors déterminer la mise de Kelly que vous devriez utiliser.

Cette méthodologie de score t peut être alambiquée, mais ses résultats sont dérivés d'un raisonnement plus intuitif de la relation entre la probabilité de victoire, la valeur attendue et la probabilité de résultat, et par extension, comment les rendements réels peuvent être considérés comme variant avec les cotes de paris. Pour les partisans de Kelly, je pense que cette méthode est plus efficace que le jalonnement de l'impact unitaire, et certainement plus efficace que l'unité de perte et l'unité de gain.